Question

【题目】如图，是平行四边形，，为的中点，且有，现以为折痕，将折起，使得点到达点的位置，且

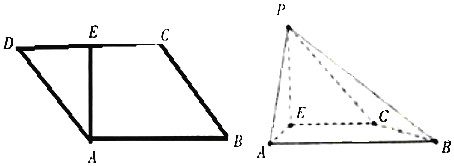
（1）证明：平面；

（2）若四棱锥的体积为，求四棱锥的侧面积．

Answer 1

【答案】（1）详见解析；（2）.

【解析】

（1）先推导出，利用线面垂直的判定定理能证明平面；（2）由四棱锥的体积为求出，由，可得平面，推导出，分别求出4个侧面的面积即可求出四棱锥的侧面积．

（1）在中，，，，

∴∠PEC=90°，即PE⊥EC，

又PE⊥AE，∴PE⊥面ABCE．

（2）由（1）得PE⊥面ABCE，

VP-ABCE=，

∴AE=1，∴PE⊥AB，又AB⊥AE，

∴AB⊥面PAE，∴AB⊥PA，∴PA=，

由题意得BC=PC=，PB=，

△PBC中，由余弦定理得，

∴∠PCB=120°，

∴，

，，

∴四棱锥P-ABCE的侧面积．