题目内容
定义:若数列 对任意
对任意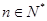 ,满足
,满足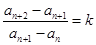 (
(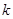 为常数),称数列
为常数),称数列 为等差比数列.
为等差比数列.
(1)若数列 前
前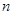 项和
项和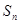 满足
满足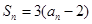 ,求
,求 的通项公式,并判断该数列是否为等差比数列;
的通项公式,并判断该数列是否为等差比数列;
(2)若数列 为等差数列,试判断
为等差数列,试判断 是否一定为等差比数列,并说明理由;
是否一定为等差比数列,并说明理由;
(3)若数列 为等差比数列,定义中常数
为等差比数列,定义中常数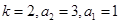 ,数列
,数列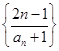 的前
的前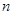 项和为
项和为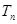 , 求证:
, 求证: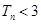 .
.
 对任意
对任意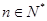 ,满足
,满足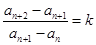 (
(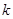 为常数),称数列
为常数),称数列 为等差比数列.
为等差比数列.(1)若数列
 前
前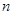 项和
项和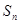 满足
满足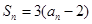 ,求
,求 的通项公式,并判断该数列是否为等差比数列;
的通项公式,并判断该数列是否为等差比数列;(2)若数列
 为等差数列,试判断
为等差数列,试判断 是否一定为等差比数列,并说明理由;
是否一定为等差比数列,并说明理由;(3)若数列
 为等差比数列,定义中常数
为等差比数列,定义中常数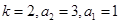 ,数列
,数列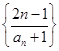 的前
的前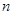 项和为
项和为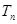 , 求证:
, 求证: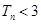 .
.(1)数列 是首项为3,公比为
是首项为3,公比为 的等比数列
的等比数列
(2)当 时,
时, 数列
数列 是等差比数列;
是等差比数列;
当 时,数列
时,数列 是常数列,数列
是常数列,数列 不是等差比数列..
不是等差比数列..
(3)
 是首项为3,公比为
是首项为3,公比为 的等比数列
的等比数列(2)当
 时,
时, 数列
数列 是等差比数列;
是等差比数列; 当
 时,数列
时,数列 是常数列,数列
是常数列,数列 不是等差比数列..
不是等差比数列..(3)

试题分析:解:(1)当
 时,
时,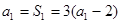 ,则
,则
当
 时,
时, ,则
,则
 数列
数列 是首项为3,公比为
是首项为3,公比为 的等比数列,
的等比数列,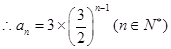

 数列
数列 是等差比数列。
是等差比数列。设等差数列
 的公差为
的公差为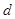 ,则
,则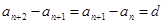 ,
,当
 时,
时, 数列
数列 是等差比数列;
是等差比数列; 当
 时,数列
时,数列 是常数列,数列
是常数列,数列 不是等差比数列.
不是等差比数列. 由

知数列
 是以2为首项,2为公比的等比数列.
是以2为首项,2为公比的等比数列.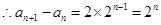 ,
,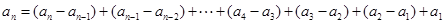
 ,
,  ①
①①
 得
得 ②
②①
 ②得
②得

点评:解决的关键是根据数列的递推关系来得到通项公式以及错位相减法求和,属于基础题。

练习册系列答案
相关题目
 的公比
的公比 ,且
,且 ,又
,又 ,那么( )
,那么( )


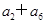 与
与 的大小不能确定
的大小不能确定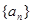 是等比数列,且
是等比数列,且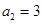 ,
,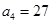
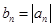 ,求
,求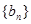 的前
的前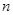 项的和
项的和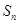
 成等比数列,且函数
成等比数列,且函数 时取到极大值
时取到极大值 ,则
,则 等于( )
等于( )



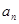 }中
}中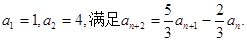
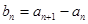 ,求证数列{
,求证数列{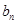 }是等比数列;
}是等比数列; 中,a1=1,且
中,a1=1,且 ,计算a2、a3、a4,并猜想
,计算a2、a3、a4,并猜想 =__________.
=__________. 项的和为
项的和为  的值。
的值。