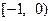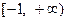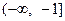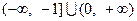题目内容
不等式(m2-2m-3)x2-(m-3)x-1<0的解集为R,求实数m的取值范围.
-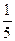 <m≤3
<m≤3
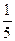 <m≤3
<m≤3解:(1)当m2-2m-3=0,即m=3或m=-1时,
①若m=3,原不等式解集为R
②若m=-1,原不等式化为4x-1<0
∴原不等式解集为{x|x<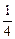 =,不合题设条件.
=,不合题设条件.
(2)若m2-2m-3≠0,依题意有
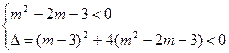 即
即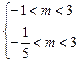
∴-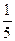 <m<3
<m<3
综上,当-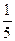 <m≤3时,不等式(m2-2m-3)x2-(m-3)x-1<0的解集为R.
<m≤3时,不等式(m2-2m-3)x2-(m-3)x-1<0的解集为R.
①若m=3,原不等式解集为R
②若m=-1,原不等式化为4x-1<0
∴原不等式解集为{x|x<
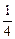 =,不合题设条件.
=,不合题设条件.(2)若m2-2m-3≠0,依题意有
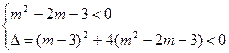 即
即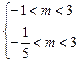
∴-
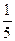 <m<3
<m<3综上,当-
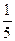 <m≤3时,不等式(m2-2m-3)x2-(m-3)x-1<0的解集为R.
<m≤3时,不等式(m2-2m-3)x2-(m-3)x-1<0的解集为R. 
练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
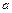 ≤
≤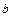 ≤
≤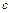 ≤1,求证:
≤1,求证: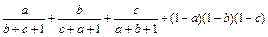 ≤1
≤1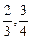 ],那么λ为何值时,能使宣传画所用纸张面积最小?
],那么λ为何值时,能使宣传画所用纸张面积最小?
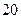 分)设
分)设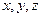 为非负实数,满足
为非负实数,满足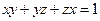 ,证明:
,证明: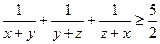 .
.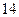
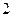 ,若这个两位数小于
,若这个两位数小于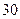 ,
,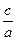 >
> 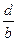 ③bc>ad以其中两个作条件余下一个作结论,则可组 个正确命题.
③bc>ad以其中两个作条件余下一个作结论,则可组 个正确命题.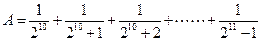 ,则
,则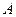 与
与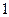 的大小关系是_____________。
的大小关系是_____________。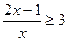 的解集为 ( )
的解集为 ( )