题目内容
6.△ABC满足BA=BC=3$\sqrt{2}$,∠ABC=120°,D在AC上,且∠DBC=30°,若$\overrightarrow{BD}$=λ1$\overrightarrow{BC}$+λ2$\overrightarrow{BA}$,求λ1+2λ2.分析 画出图形,根据条件可以得到∠ABD=90°,∠BAD=30°,然后对$\overrightarrow{BD}={λ}_{1}\overrightarrow{BC}+{λ}_{2}\overrightarrow{BA}$的两边分别乘以向量$\overrightarrow{BC},\overrightarrow{BA}$,然后进行向量数量积的运算便可得到关于λ1,λ2的二元一次方程组,解出λ1,λ2从而便可得出λ1+2λ2.
解答 解:如图,根据条件得,∠ABD=90°,∠BAD=30°;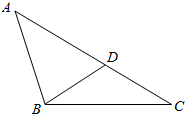
∴BD=AB•tan30°=3$\sqrt{2}$$•\frac{\sqrt{3}}{3}$=$\sqrt{6}$;
∴在$\overrightarrow{BD}={λ}_{1}\overrightarrow{BC}+{λ}_{2}\overrightarrow{BA}$两边分别乘以$\overrightarrow{BC},\overrightarrow{BA}$得:$\left\{\begin{array}{l}{\overrightarrow{BD}•\overrightarrow{BC}={λ}_{1}{\overrightarrow{BC}}^{2}+{λ}_{2}\overrightarrow{BA}•\overrightarrow{BC}}\\{\overrightarrow{BD}•\overrightarrow{BA}={λ}_{1}\overrightarrow{BC}•\overrightarrow{BA}+{λ}_{2}{\overrightarrow{BA}}^{2}}\end{array}\right.$;
∴$\left\{\begin{array}{l}{\sqrt{6}•3\sqrt{2}•\frac{\sqrt{3}}{2}=18{λ}_{1}-9{λ}_{2}}\\{0=-9{λ}_{1}+18{λ}_{2}}\end{array}\right.$;
解得,${λ}_{1}=\frac{2}{3},{λ}_{2}=\frac{1}{3}$;
∴${λ}_{1}+2{λ}_{2}=\frac{4}{3}$.
点评 考查向量数量积的运算及其计算公式,向量垂直的充要条件,以及正切函数的定义.

| A. | (k,$\frac{k+1}{k-1}$] | B. | (1,$\frac{k+1}{k-1}$] | C. | (1,k] | D. | [k,+∞) |
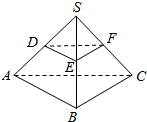 如图所示,正三棱锥S-ABC中,D,E,F分别是棱SA,SB,SC上的点,且SD=a,平面DEF∥底面ABC,且三棱台DEF-ABC与三棱锥S-ABC的所有棱长之和相等,则三棱锥S-DEF的外接球的表面积为$\frac{3π}{2}$a2.
如图所示,正三棱锥S-ABC中,D,E,F分别是棱SA,SB,SC上的点,且SD=a,平面DEF∥底面ABC,且三棱台DEF-ABC与三棱锥S-ABC的所有棱长之和相等,则三棱锥S-DEF的外接球的表面积为$\frac{3π}{2}$a2.