题目内容
15.求函数f(x)=$\frac{sin\frac{5}{2}x}{2sin\frac{x}{2}}$-$\frac{1}{2}$的值域.分析 先将函数式化为f(x)=2(cosx+$\frac{1}{4}$)2-$\frac{9}{8}$的形式,再结合cosx的范围,求得函数f(x)的值域.
解答 解:f(x)=$\frac{sin\frac{5}{2}x}{2sin\frac{x}{2}}$-$\frac{1}{2}$=$\frac{sin\frac{5x}{2}-sin\frac{x}{2}}{2sin\frac{x}{2}}$
=$\frac{1}{2sin\frac{x}{2}}$•[sin($\frac{3x}{2}$+x)-sin($\frac{3x}{2}$-x)]
=$\frac{1}{2sin\frac{x}{2}}$•2•cos$\frac{3x}{2}$•sinx,
=2•cos$\frac{x}{2}$•cos$\frac{3x}{2}$=cos2x+cosx
=2cos2x+cosx-1
=2(cosx+$\frac{1}{4}$)2-$\frac{9}{8}$,所以,
①当cosx=-$\frac{1}{4}$时,函数f(x)取得最小值-$\frac{9}{8}$;
②当cosx=1时,函数f(x)取得最大值2,
故函数f(x)的值域为:[-$\frac{9}{8}$,2].
点评 本题主要考查了三角函数的恒等变换,涉及两角和差的三角函数,倍角公式,以及运用配方法求函数最值,属于中档题.

练习册系列答案
相关题目
20.已知函数f(x)满足其导函数f′(x)=1-πsinπx,且f(1)=-2,则f($\frac{1}{2016}$)十f($\frac{2}{2016}$)+f($\frac{3}{2016}$)+…+f($\frac{2014}{2016}$)+f($\frac{2015}{2016}$),的值为( )
| A. | 1 | B. | 0 | C. | $\frac{6045}{2}$ | D. | -$\frac{6045}{2}$ |
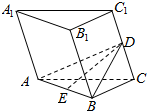 在正三棱柱ABC-A1B1C1中,E是AB的中点,D是CC1上一点.
在正三棱柱ABC-A1B1C1中,E是AB的中点,D是CC1上一点.