题目内容
(本小题满分12分) 过圆 上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.
上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)设点P关于 的对称点为E,关于
的对称点为E,关于 的对称点为F,求|EF|的取值范围.
的对称点为F,求|EF|的取值范围.
 上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.
上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.(Ⅰ)求点P的轨迹方程;
(Ⅱ)设点P关于
 的对称点为E,关于
的对称点为E,关于 的对称点为F,求|EF|的取值范围.
的对称点为F,求|EF|的取值范围.(1)连结PC,由垂径分弦定理知,PC⊥AB,所以点P的轨迹是以线段AC为直径的圆(除去点A).因为点A(4,6),C(6,4),则其中点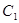 坐标为(5,5),又圆半径
坐标为(5,5),又圆半径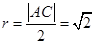 .
.
故点P的轨迹方程是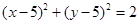 (x≠4,y≠6).(4分)
(x≠4,y≠6).(4分)
(2)设点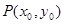 ,因为点P、E关于x=1对称,,则点
,因为点P、E关于x=1对称,,则点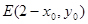
因为P、F关于y=x对 称,则点F
称,则点F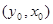 (6分)
(6分)
所以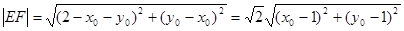
设点M(1,1),则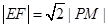 .
. 
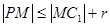
即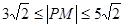 ,所以
,所以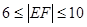 (12分)
(12分)
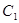 坐标为(5,5),又圆半径
坐标为(5,5),又圆半径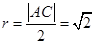 .
.故点P的轨迹方程是
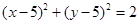 (x≠4,y≠6).(4分)
(x≠4,y≠6).(4分) (2)设点
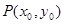 ,因为点P、E关于x=1对称,,则点
,因为点P、E关于x=1对称,,则点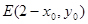
因为P、F关于y=x对
 称,则点F
称,则点F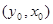 (6分)
(6分) 所以
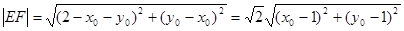
设点M(1,1),则
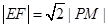 .
. 
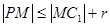
即
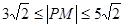 ,所以
,所以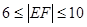 (12分)
(12分)略

练习册系列答案
相关题目
 上,且与直线
上,且与直线 相切于点
相切于点 的圆的方程.
的圆的方程. 外切于(2,4)点且半径为
外切于(2,4)点且半径为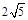 的圆的方程.
的圆的方程.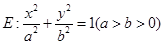 过点
过点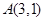 ,左、右焦点分别为
,左、右焦点分别为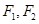 ,离心率为
,离心率为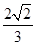 ,经过
,经过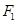 的直线
的直线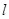 与圆心在
与圆心在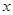 轴上且经过点
轴上且经过点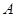 的圆
的圆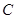 恰好相切于点
恰好相切于点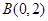 .
.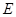 及圆
及圆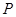 ,使
,使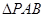 为以
为以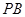 为底边的等腰三角形?若存在,求点
为底边的等腰三角形?若存在,求点
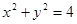 ,P是圆O上的一个动点,若线段OP的垂直平分线总是被平面区域
,P是圆O上的一个动点,若线段OP的垂直平分线总是被平面区域 覆盖,则实数
覆盖,则实数 的取值范围是()
的取值范围是()



 、
、 是
是 的切线,切点分别为
的切线,切点分别为 、
、 ,点
,点 在
在 ,那么
,那么 等于( )
等于( )


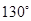
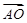 ·
·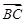 的值( )
的值( )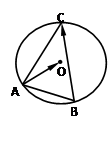
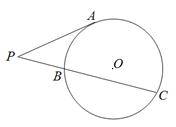
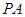 是圆
是圆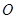 的切线,
的切线,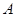 为切点,
为切点,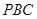 是圆
是圆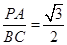 ,则
,则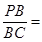 ______.
______.
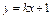 与曲线
与曲线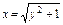 有两个不同的交点,则k的取值范围是_____
有两个不同的交点,则k的取值范围是_____