已知数列{an}.a1=$\frac{1}{2}$.且满足2an+1=1-$\frac{{a} {n+1}}{{a} {n}}$．(1)求证:数列{$\frac{1}{{a} {n}}$}是等差数列,(2)设bn=anan+1.求数列{bn}的前n项和Sn．题目和参考答案——青夏教育精英家教网—

题目内容

11．已知数列{a_n}，a₁=$\frac{1}{2}$，且满足2a_n+1=1-$\frac{{a}_{n+1}}{{a}_{n}}$．
（1）求证：数列{$\frac{1}{{a}_{n}}$}是等差数列；
（2）设b_n=a_na_n+1，求数列{b_n}的前n项和S_n．

分析（1）通过2a_n+1=1-$\frac{{a}_{n+1}}{{a}_{n}}$，可得2a_n+1a_n=a_n-a_n+1，进而有2=$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$；
（2）通过（1）知a_n=$\frac{1}{2}$•$\frac{1}{n}$，分离分母可得b_n=$\frac{1}{4}$•（$\frac{1}{n}$-$\frac{1}{n+1}$），并项相加即可．

解答（1）证明：∵2a_n+1=1-$\frac{{a}_{n+1}}{{a}_{n}}$，∴2a_n+1a_n=a_n-a_n+1，
两边同除以a_n+1a_n得：2=$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$，
又a₁=$\frac{1}{2}$，∴$\frac{1}{{a}_{1}}$=2，
∴数列{$\frac{1}{{a}_{n}}$}是首项和公差均为2的等差数列；
（2）解：由（1）知$\frac{1}{{a}_{n}}$=2n，∴a_n=$\frac{1}{2}$•$\frac{1}{n}$，
∴b_n=a_na_n+1=$\frac{1}{4}$•$\frac{1}{n（n+1）}$=$\frac{1}{4}$•（$\frac{1}{n}$-$\frac{1}{n+1}$），
∴S_n=$\frac{1}{4}$•（1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$）=$\frac{1}{4}$•（1-$\frac{1}{n+1}$）=$\frac{1}{4}$•$\frac{n}{n+1}$．

点评本题考查数列的递推公式，对表达式的灵活变形、分离分母、并项相加是解决本题的关键，注意解题方法的积累，属于中档题．

练习册系列答案

2．已知数列{a_n}满足a_n=n•kⁿ（n∈N^*，0＜k＜1）给出下列命题：
①当k=$\frac{1}{2}$时，数列{a_n}为递减数列
②当$\frac{1}{2}$＜k＜1时，数列{a_n}不一定有最大项
③当0＜k＜$\frac{1}{2}$时，数列{a_n}为递减数列
④当$\frac{k}{1-k}$为正整数时，数列{a_n}必有两项相等的最大项
其中真命题的个数为（　　）

19．

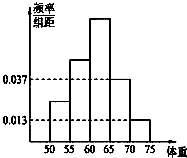为了解今年某校高三毕业班准备报考飞行员学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，其中第2小组的频数为12．
（Ⅰ）求该校报考飞行员的总人数；
（Ⅱ）从这所学校报考飞行员的同学中任选一人，求这个人体重超过60公斤的概率．

6．直线l过抛物线C：y²=4x的焦点且与x轴垂直，则l与C所围成的图形的面积等于$\frac{8}{3}$．

16．已知x、y均为实数，记max{x，y}=$\left\{\begin{array}{l}{x，x≥y}\\{y，x＜y}\end{array}\right.$，min{x，y}=$\left\{\begin{array}{l}{y，x≥y}\\{x，x＜y}\end{array}\right.$．若i表示虚数单位，且a=x₁+y₁i，b=x₂+y₂i，x₁，y₁，x₂，y₂∈R，则（　　）

	A．	min{\|a+b\|，\|a-b\|}≤min{\|a\|，\|b\|}		B．	max{\|a+b\|，\|a-b\|}≤max{\|a\|，\|b\|}
	C．	min{\|a+b\|²，\|a-b\|²}≥\|a\|²+\|b\|²		D．	max{\|a+b\|²，\|a-b\|²}≥{\|a\|²+\|b\|²