题目内容
已知函数 .
.
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ) 若存在实数 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(Ⅰ) 的单调递减区间是
的单调递减区间是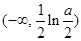 ,单调递增区间是
,单调递增区间是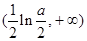 .
.
(Ⅱ) (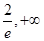 ).
).
解析试题分析:(Ⅰ)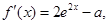
(ⅰ)当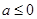 时,
时, 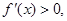

 的单调递增区间是(
的单调递增区间是(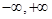 ).
).
(ⅱ) 当 时,令
时,令 得
得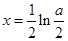
当 时,
时,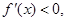 当
当 时,
时,
 的单调递减区间是
的单调递减区间是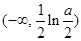 ,
, 的单调递增区间是
的单调递增区间是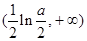 . 6分
. 6分
(Ⅱ)由 ,
,
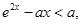
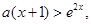
由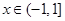 得
得 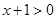 .
. 
 设
设 ,若存在实数
,若存在实数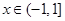 ,使得
,使得 成立, 则
成立, 则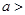
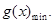 10分
10分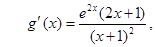 由
由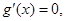 得
得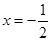 ,
, 当
当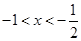 时,
时,  当
当 时,
时, 

 在
在 上是减函数,在
上是减函数,在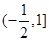 上是增函数.
上是增函数. 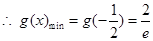
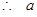 的取值范围是(
的取值范围是(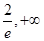 ). 14分
). 14分
考点:本题主要考查应用导数研究函数的单调性及极(最)值,研究函数的图象和性质,不等式恒成立问题。
点评:难题,不等式恒成立问题,常常转化成求函数的最值问题。(II)小题,通过构造函数,研究函数的单调性、极值(最值),进一步确定得到参数的范围。

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
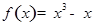 .
. 在点
在点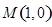 处的切线方程;
处的切线方程;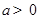 ,如果过点
,如果过点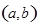 可作曲线
可作曲线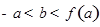

 。
。 的最小值;
的最小值; 
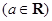 ,讨论函数
,讨论函数 的单调性;
的单调性; 的直线与曲线
的直线与曲线 交于
交于 ,
,
 两点,求证:
两点,求证: 。
。 ,直线x+y=3以及两坐标轴所围成的图形的面积S.
,直线x+y=3以及两坐标轴所围成的图形的面积S.
 ,
, 取得极值,求实数
取得极值,求实数 的值;
的值; 时,求
时,求 上的最小值;
上的最小值; ,直线
,直线 都不是曲线
都不是曲线 的切线,求实数
的切线,求实数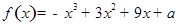 在区间[-2,2]的最大值为20,求它在该区间的最小值。
在区间[-2,2]的最大值为20,求它在该区间的最小值。
 在
在 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围; 时,求
时,求 上的最大值和最小值.
上的最大值和最小值. ,
, .求函数
.求函数 的单调递减区间;
的单调递减区间; 在
在 上是增函数.
上是增函数. .
. 在点
在点 处的切线方程;
处的切线方程; ,如果过点
,如果过点 可作曲线
可作曲线