题目内容
设函数
 。
。
(1)求函数 的最小值;
的最小值;
(2)设
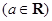 ,讨论函数
,讨论函数 的单调性;
的单调性;
(3)斜率为 的直线与曲线
的直线与曲线 交于
交于 ,
,
 两点,求证:
两点,求证: 。
。
(1)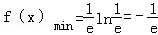 .(2)当a≥0时,F(x)在(0,+∞)上是增函数;
.(2)当a≥0时,F(x)在(0,+∞)上是增函数;
当a<0时,F(x)在 上单调递增,在
上单调递增,在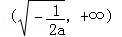 上单调递减.(3)构造函数利用函数的单调性证明不等式
上单调递减.(3)构造函数利用函数的单调性证明不等式
解析试题分析:(1)f'(x)=lnx+1(x>0),令f'(x)=0,得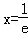 .
.
∵当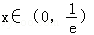 时,f'(x)<0;当
时,f'(x)<0;当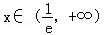 时,
时,
f'(x)>0,
∴当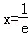 时,
时,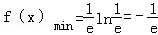 . 4分
. 4分
(2)F(x)=ax2+lnx+1(x>0),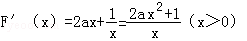 .
.
①当a≥0时,恒有F'(x)>0,F(x)在(0,+∞)上是增函数;
②当a<0时,
令F'(x)>0,得2ax2+1>0,解得 ;
;
令F'(x)<0,得2ax2+1<0,解得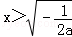 .
.
综上,当a≥0时,F(x)在(0,+∞)上是增函数;
当a<0时,F(x)在 上单调递增,在
上单调递增,在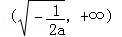 上单调递减. 8分
上单调递减. 8分
(3)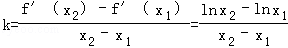 .
.
要证 ,即证
,即证 ,等价于证
,等价于证 ,令
,令 ,
,
则只要证 ,由t>1知lnt>0,
,由t>1知lnt>0,
故等价于证lnt<t﹣1<tlnt(t>1)(*).
①设g(t)=t﹣1﹣lnt(t≥1),则 ,
,
故g(t)在[1,+∞)上是增函数,
∴当t>1时,g(t)=t﹣1﹣lnt>g(1)=0,即t﹣1>lnt(t>1).
②设h(t)=tlnt﹣(t﹣1)(t≥1),则h'(t)=lnt≥0(t≥1),故h(t)在[1,+∞)上是增函数,
∴当t>1时,h(t)=tlnt﹣(t﹣1)>h(1)=0,即t﹣1<tlnt(t>1).
由①②知(*)成立,得证. 12分
考点:本题考查了导数的运用
点评:导数本身是个解决问题的工具,是高考必考内容之一,高考往往结合函数甚至是实际问题考查导数的应用,求单调、最值、完成证明等,请注意归纳常规方法和常见注意点

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案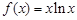 .
.  的最小值;
的最小值;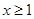 都有
都有 ,求实数
,求实数 的取值范围.
的取值范围. 若存在函数
若存在函数 使得
使得 恒成立,则称
恒成立,则称 的一个“下界函数”.
的一个“下界函数”. 为实数
为实数 为
为 的取值范围;
的取值范围; 试问函数
试问函数 是否存在零点,若存在,求出零点个数;若不存在,请说明理由.
是否存在零点,若存在,求出零点个数;若不存在,请说明理由. (
( ,b∈Z),曲线
,b∈Z),曲线 在点(2,
在点(2, )处的切线方程为
)处的切线方程为 =3.
=3.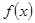 的解析式;
的解析式; 和直线
和直线 所围三角形的面积为定值,并求出此定值.
所围三角形的面积为定值,并求出此定值. ;
; 在
在 上单调递增,在
上单调递增,在 上单调递减,在
上单调递减,在 上单调递增,求实数
上单调递增,求实数 的值;
的值; 时,求证:当
时,求证:当 时,
时,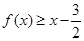 .
.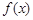 的导函数是
的导函数是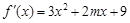 ,
,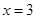 处取得极值,且
处取得极值,且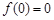 ,
, 上的最大值为
上的最大值为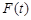 ,若对任意的
,若对任意的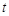
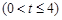 总有
总有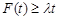 成立,求
成立,求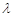 的取值范围;
的取值范围;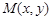 是曲线
是曲线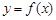 上的任意一点.当
上的任意一点.当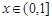 时,求直线OM斜率的最
时,求直线OM斜率的最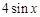 的大小关系,并说明理由.
的大小关系,并说明理由. ,其中
,其中 。
。 有极值
有极值 ,求
,求 的值;
的值; 在区间
在区间 上为增函数,求
上为增函数,求
 .
. 的单调区间;
的单调区间; ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围. 在区间
在区间 上最大值是5,最小值是-11,求
上最大值是5,最小值是-11,求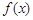 的解析式.
的解析式.