题目内容
已知函数 ,
,
(1)若x=1时 取得极值,求实数
取得极值,求实数 的值;
的值;
(2)当 时,求
时,求 在
在 上的最小值;
上的最小值;
(3)若对任意 ,直线
,直线 都不是曲线
都不是曲线 的切线,求实数
的切线,求实数 的取值范围。
的取值范围。
(1) (2)
(2)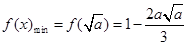 (3)
(3)
解析试题分析:(1)∵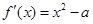 ,∴
,∴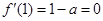 ,得
,得
当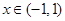 时,
时,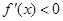 ; 当
; 当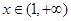 时,
时,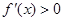 。
。
∴ 在
在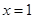 时取得极小值,故
时取得极小值,故 符合。
符合。
(2)当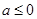 时,
时,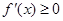 对
对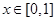 恒成立,
恒成立, 在
在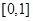 上单调递增,
上单调递增,
∴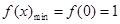
当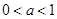 时,由
时,由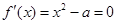 得
得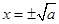 ,
,
若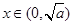 ,则
,则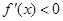 ,∴
,∴ 在
在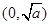 上单调递减。
上单调递减。
若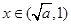 ,则
,则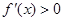 ,∴
,∴ 在
在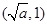 上单调递增。
上单调递增。
∴ 在
在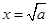 时取得极小值,也是最小值,即
时取得极小值,也是最小值,即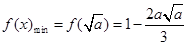 。
。
综上所述,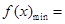

(3)∵任意 ,直线
,直线 都不是曲线
都不是曲线 的切线,
的切线,
∴ 对
对 恒成立,即
恒成立,即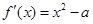 的最小值大于
的最小值大于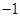 ,
,
而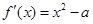 的最小值为
的最小值为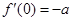 ,∴
,∴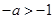 ,故
,故 .
.
考点:利用导数求闭区间上函数的最值;利用导数研究函数的极值.
点评:深刻理解导数的几何意义及熟练利用导数求极值、最值是解题的关键.分类讨论思想和转化思想是解题常用的思想方法,应熟练掌握.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 有极值,
有极值, 的取值范围;
的取值范围; ;
; 在
在 上单调递增,在
上单调递增,在 上单调递减,在
上单调递减,在 上单调递增,求实数
上单调递增,求实数 的值;
的值; 时,求证:当
时,求证:当 时,
时,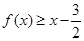 .
. ,其中
,其中 。
。 有极值
有极值 ,求
,求 的值;
的值; 在区间
在区间 上为增函数,求
上为增函数,求
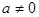 ,函数
,函数 .
. 有极大值32,求实数
有极大值32,求实数 的值;
的值; ,不等式
,不等式 恒成立,求实数
恒成立,求实数 .
. 的单调区间;
的单调区间; ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围. 在点
在点 处的切线与x轴交点的横坐标为an.
处的切线与x轴交点的横坐标为an. ,求数到
,求数到 的前n项和Sn.
的前n项和Sn. ,
, 所围成的封闭图形的面积
所围成的封闭图形的面积 在(-∞,+∞)上是增函数.
在(-∞,+∞)上是增函数.