[题目]已知函数()．(1)若曲线在点处的切线与直线垂直.求函数的单调区间,(2)若对于任意.都有成立.试求a的取值范围．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知函数（）．

（1）若曲线在点处的切线与直线垂直，求函数的单调区间；

（2）若对于任意，都有成立，试求a的取值范围．

【答案】（1）单调增区间是，单调减区间是．（2）.

【解析】

（1）对求导，由曲线在点处的切线与直线垂直，可得，可得值，代入可得函数的单调区间；

（2）对求导，可得其递增递减区间，可得其极小值点，函数取得最小值，由对于任意,成立，只需最小值大于，可得a的取值范围.

解：（1）直线的斜率为1，函数的定义域为．

因为，

所以，所以，

所以，．

由解得；由解得．

所以的单调增区间是，单调减区间是．

（2）

由解得；由解得．

所以在区间上单调递增，在区间上单调递减，

所以当时，函数取得最小值．

因为对于任意都有成立，

只需即可．

则，

即，解得，

所以a的取值范围是．

练习册系列答案

将学生在一周时间内进行网络搜题频数超过20次的行为视为“经常使用网络搜题”，不超过20次的视为“偶尔或不用网络搜题”.

（1）根据已有数据，完成下列列联表（单位：人）中数据的填写，并判断是否在犯错误的概率不超过1%的前提下有把握认为使用网络搜题与性别有关？

（2）将上述调查所得到的频率视为概率，从该校所有参与调查的学生中，采用随机抽样的方法每次抽取一个人，抽取4人，记经常使用网络搜题的人数为，若每次抽取的结果是相互独立的，求随机变量的分布列和数学期望.

参考公式：，其中.

参考数据：

【题目】《朗读者》是一档文化情感类节目，以个人成长、情感体验、背景故事与传世佳作相结合的方式，选用精美的文字，用最平实的情感读出文字背后的价值，深受人们的喜爱.为了了解人们对该节目的喜爱程度，某调查机构随机调查了，两个城市各100名观众，得到下面的列联表.

	非常喜爱	喜爱	合计
城市	60		100
城市		30
合计			200

完成上表，并根据以上数据，判断是否有的把握认为观众的喜爱程度与所处的城市有关？

附参考公式和数据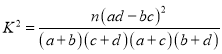：（其中）.

	0.15	0.10	0.05	0.025	0.010
	2.072	2.706	3.841	5.024	6.635

【题目】已知函数，其中.

（1）当时，求曲线在点处切线的方程；

（2）当时，求函数的单调区间；

【题目】设，。

（1）求的单调区间；

（2）讨论零点的个数；

（3）当时，设恒成立，求实数的取值范围.

【题目】某快递公司在某市的货物转运中心，拟引进智能机器人分拣系统，以提高分拣效率和降低物流成本，已知购买x台机器人的总成本p(x)＝万元．

(1)若使每台机器人的平均成本最低，问应买多少台？

(2)现按(1)中的数量购买机器人，需要安排m人将邮件放在机器人上，机器人将邮件送达指定落袋格口完成分拣，经实验知，每台机器人的日平均分拣量q(m)＝ (单位：件)，已知传统人工分拣每人每日的平均分拣量为1200件，问引进机器人后，日平均分拣量达最大值时，用人数量比引进机器人前的用人数量最多可减少百分之几？