题目内容
20.下列命题中不正确的是( )| A. | 用平行于圆锥底面的平面截圆锥,截面和底面之间的部分是圆台 | |
| B. | 以直角梯形的一腰为旋转轴,另一腰为母线的旋转面是圆台的侧面 | |
| C. | 圆锥、圆柱、圆台的底面都是圆 | |
| D. | 圆台的母线延长后与轴交于同一点 |
分析 根据圆锥,圆台,圆柱的几何特征,逐一分析四个命题的真假可得答案.
解答 解:用平行于圆锥底面的平面截圆锥,截面和底面之间的部分是圆台,故A正确;
以直角梯形的直角腰为旋转轴,另一腰为母线的旋转面是圆台的侧面,故B错误;
圆锥、圆柱、圆台的底面都是圆,故C正确;
圆台的母线延长后与轴交于同一点,故D正确;
故选:B
点评 本题以命题的真假判断与应用为载体,考查了旋转体的几何特征,难度不大,属于基础题.

练习册系列答案
相关题目
5.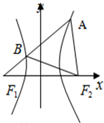 如图,F1、F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点A、B.若△ABF2为等边三角形,则双曲线的离心率为( )
如图,F1、F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点A、B.若△ABF2为等边三角形,则双曲线的离心率为( )
 如图,F1、F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点A、B.若△ABF2为等边三角形,则双曲线的离心率为( )
如图,F1、F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点A、B.若△ABF2为等边三角形,则双曲线的离心率为( )| A. | 4 | B. | $\sqrt{7}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
9.已知P(2,4)在双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的渐近线上,则该双曲线的离心率为( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
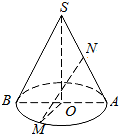 已知圆锥的底面半径r=2,半径OM与母线SA垂直,N是SA中点,NM与高SO所成的角为α,tanα=2.则圆锥的体积为$\frac{4\sqrt{5}}{3}π$.
已知圆锥的底面半径r=2,半径OM与母线SA垂直,N是SA中点,NM与高SO所成的角为α,tanα=2.则圆锥的体积为$\frac{4\sqrt{5}}{3}π$.