题目内容
10.关于x的不等式|x-1|>a+1(a∈R)的解集为A.(1)若a=1,解不等式;
(2)求A;
(3)B={x|x=2k-1,k∈Z},若CRA∩B中有且只有5个元素.求a的范围.
分析 (1)a=1时,关于x的不等式即|x-1|>2,由此求得x的范围.
(2)分类讨论a的值,分a<-1、a=-1、a>-1三种情况,分别求得A.
(3)B={x|x=2k-1,k∈Z}表示奇数集合,再分当a<-1、a=-1、a>-1三种情况,分别求得a的范围,综合可得结论.
解答 解:(1)a=1时,关于x的不等式即|x-1|>2,即x-1<-2 或x-1>2,
求得它的解集为{x|x<-1 或x>3}.
(2)当a<-1时,a+1<0,不等式|x-1|>a+1(a∈R)的解集为A=R;
当a=-1时,不等式|x-1|>0的解集为A={x|x≠1};
当a>-1时,a+1>0,由|x-1|>a+1,可得x-1>a+1,或x-1<-a-1,
求得它的解集为{x|x>a+2,或 x<-a}.
(3)B={x|x=2k-1,k∈Z}表示奇数集合,当a<-1,若CRA=∅,不满足CRA∩B中有且只有5个元素;
当a=-1时,A={1},不满足当CRA∩B中有且只有5个元素;
当a>-1时,CRA=[-a,a+2],故[-a,a+2]中含有5个奇数,
而这5个奇数的间距为8,如:1,3,5,7,9,
故a+2-(-a)≥8,求得a≥3.
综上可得,a≥3.
点评 本题主要考查绝对值三角不等式,绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
15.设a=${log}_{\frac{1}{5}}$3,b=($\frac{1}{3}$)0.4,c=4${\;}^{\frac{1}{3}}$,则( )
| A. | c>b>a | B. | c>a>b | C. | b>a>c | D. | a>b>c |
20.下列命题中不正确的是( )
| A. | 用平行于圆锥底面的平面截圆锥,截面和底面之间的部分是圆台 | |
| B. | 以直角梯形的一腰为旋转轴,另一腰为母线的旋转面是圆台的侧面 | |
| C. | 圆锥、圆柱、圆台的底面都是圆 | |
| D. | 圆台的母线延长后与轴交于同一点 |
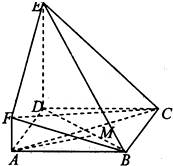 如图,ABCD是边长为3的正方形,AF∥DE,DE=3AF.
如图,ABCD是边长为3的正方形,AF∥DE,DE=3AF.