题目内容
【题目】已知正方体
的棱长为2，点
，
，
分别为棱
，
，
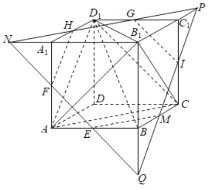
的中点，下列结论中，其中正确的个数是（ ）
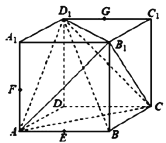
①过，，三点作正方体的截面，所得截面为正六边形；
②
平面
；
③
平面
；
④异面直线
与
所成角的正切值为
；
⑤四面体
的体积等于
A.1B.2C.3D.4
【答案】B
【解析】
根据公理3，作截面可知①正确；根据直线与平面的位置关系可知②不正确；根据线面垂直的判定定理可知③正确；由条件有
,所以
为异面直线
与
的夹角可知④正确；用正方体体积减去四个正三棱锥的体积可知⑤不正确．
对于①.延长分别与
的延长线交于
，连接
交
于
，设
与
的延长线交于
，连接
交
于
，交
于
，连
，则截面六边形
为正六边形，故①正确；
对于②.
与相交，故与平面
相交，所以②不正确；
对于③.∵
，且
与
相交，所以
平面
，故③正确；
对于④.连接
,由条件有,所以（或其补角）为异面直线与的夹角,在直角三角形
中，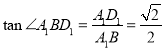
.故④不正确；
对于⑤.四面体
的体积等于正方体的体积减去四个正三棱锥的体积，即为
，故⑤不正确．
所以正确的命题有2个.
故选：B
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】随着智能手机的普及，手机计步软件迅速流行开来，这类软件能自动记载每个人每日健步的步数，从而为科学健身提供一定的帮助.某市工会为了解该市市民每日健步走的情况，从本市市民中随机抽取了2000名市民（其中不超过40岁的市民恰好有1000名），利用手机计步软件统计了他们某天健步的步数，并将样本数据分为
，
，
，
，
，
，
，
，
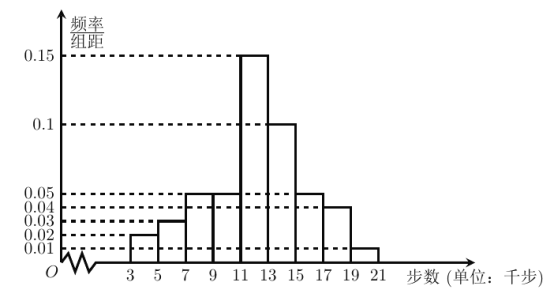
九组（单位；千步），将抽取的不超过40岁的市民的样本数据绘制成频率分布直方图如图，将40岁以上的市民的样本数据绘制成频数分布表如下，并利用该样本的频率分布估计总体的概率分布.
分组（单位 千步） |
|
|
|
|
|
|
|
|
|
频数 | 10 | 20 | 20 | 30 | 400 | 200 | 200 | 100 | 20 |
（1）现规定，日健步步数不低于13000步的为“健步达人”，填写下面列联表，并根据列联表判断能否有99.9%的把握认为是否为“健步达人”与年龄有关；
健步达人 | 非健步达人 | 总计 | |
40岁以上的市民 | |||
不超过40岁的市民 | |||
总计 |
（2）利用样本平均数和中位数估计该市不超过40岁的市民日健步步数（单位：千步）的平均数和中位数；
（3）若日健步步数落在区间
内，则可认为该市民”运动适量”，其中
，
分别为样本平均数和样本标准差，计算可求得频率分布直方图中数据的标准差约为3.64.若一市民某天的健步步数为2万步，试判断该市民这天是否“运动适量”？
参考公式：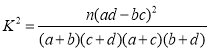
.
参考数据：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】千百年来，我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化，总结了丰富的“看云识天气”的经验，并将这些经验编成谚语，如“天上钩钩云，地上雨淋淋”“日落云里走，雨在半夜后”……小波同学为了验证“日落云里走，雨在半夜后”，观察了所在地区
的
天日落和夜晚天气，得到如下
列联表：
夜晚天气日落云里走 | 下雨 | 未下雨 |
出现 |
|
|
未出现 |
|
|
参考公式：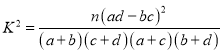
.
临界值表：
|
|
|
|
|
|
|
|
|
|
（1）根据上面的列联表判断能否有
的把握认为“当晚下雨”与“‘日落云里走’出现”有关？
（2）小波同学为进一步认识其规律，对相关数据进行分析，现从上述调查的“夜晚未下雨”天气中按分层抽样法抽取
天，再从这天中随机抽出
天进行数据分析，求抽到的这天中仅有
天出现“日落云里走”的概率．
