题目内容
【题目】设函数![]() .
.
(1)若![]() ,
,![]() ,求函数
,求函数![]() 的极值;
的极值;
(2)若![]() 是函数
是函数![]() 的一个极值点,试求出
的一个极值点,试求出![]() 关于
关于![]() 的关系式(即用
的关系式(即用![]() 表示
表示![]() ),并确定
),并确定![]() 的单调区间;(提示:应注意对
的单调区间;(提示:应注意对![]() 的取值范围进行讨论)
的取值范围进行讨论)
(3)在(2)的条件下,设![]() ,函数
,函数![]() ,若存在
,若存在![]() 使得
使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() ,见解析; (3)
,见解析; (3)![]() .
.
【解析】
(1)求出导函数的根,判断根左右两边导函数的符号,得到函数的单调性,据极大值极小值的定义求出极值;(2)据极值点处的导函数值为0得到a,b的关系;代入导函数中求出导函数的两根,讨论两根的大小;判断根左右两边导函数的符号,据导函数与单调性的关系求出单调区间;(3)据函数的单调性求出两个函数的值域,求出函数值的最小距离,最小距离小于1求出a的范围
(1)∵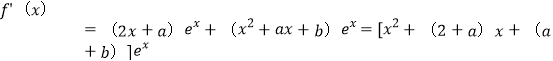
当![]() ,
,![]() 时,
时,![]() 则
则![]()
令![]() 得
得![]() ,∵
,∵![]() ∴
∴![]() ,解得
,解得![]() ,
,![]()
∵当![]() 时,
时,![]() ,当
,当![]() 时
时![]() ,当
,当![]() 时
时![]()
∴当![]() 时,函数
时,函数![]() 有极大值,
有极大值,![]() ,
,
当![]() 时,函数
时,函数![]() 有极小值,
有极小值,![]() .
.
(2)由(1)知![]()
∵![]() 是函数
是函数![]() 的一个极值点
的一个极值点
∴![]() ,即
,即![]() ,解得
,解得![]() ,
,
则![]()
令![]() ,得
,得![]() 或
或![]()
∵![]() 是极值点,∴
是极值点,∴![]() ,即
,即![]()
当![]() 即
即![]() 时,由
时,由![]() 得
得![]() 或
或![]()
由![]() 得
得![]()
当![]() 即
即![]() 时,由
时,由![]() 得
得![]() 或
或![]()
由![]() 得
得![]()
综上可知:当![]() 时,单调递增区间为
时,单调递增区间为![]() 和
和![]() ,递减区间为
,递减区间为![]()
当![]() 时,单调递增区间为
时,单调递增区间为![]() 和
和![]() ,递减区间为
,递减区间为![]()
(3)由(2)知,当![]() 时,
时,![]() 在区间
在区间![]() 上的单调递减,在区间
上的单调递减,在区间![]() 上单调递增,
上单调递增,
∴函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]()
又∵![]() ,
,![]() ,
,
∴函数![]() 在区间
在区间![]() 上的值域是
上的值域是![]() ,即
,即![]()
又![]() 在区间
在区间![]() 上是增函数,
上是增函数,
且它在区间![]() 上的值域是
上的值域是![]()
∵![]() ,
,
∴存在![]() 使得
使得![]()
成立只须仅须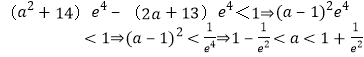 .
.

【题目】某高校在2019年的冬令营考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下图所示:
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| 35 | 0.350 |
第3组 |
| 10 | 0.100 |
第4组 |
| 20 | 0.200 |
第5组 |
| 30 | 0.300 |
合计 | 100 | 1.00 | |
(1)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(2)在(1)的前提下,高校决定在这6名学生中,随机抽取2名学生接受A考官进行面试,求第4组至少有一名学生被A考官测试的概率.