题目内容
【题目】设
为平面直角坐标系xOy中的点集，从中的任意一点P作x轴、y轴的垂线，垂足分别为M,N,记点M的横坐标的最大值与最小值之差为x(),点N的纵坐标的最大值与最小值之差为y().若是边长为1的正方形，给出下列三个结论:
①x(Q)的最大值为
②x(Q)+y(Q)的取值范围是
③x(Q)-y(Q)恒等于0.
其中所有正确结论的序号是_________
【答案】①②③．
【解析】
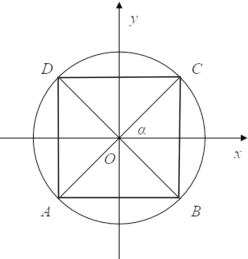
易得
与正方形
的位置无关,故可以考虑将正方形确定在原点,再绕着原点旋转分析所有情况即可.
如图由题易得与正方形的位置无关,故将正方形
确定在原点,则只需考虑当正方形绕着原点旋转的所有情况即可.此时对角线长
.当正方形边均平行于坐标轴时取最小值
.且
对①,
,故①正确
对②, 
,故②正确.
对③,因为,故
,故③正确.
故答案为：①②③
练习册系列答案
相关题目
