题目内容
【题目】已知函数![]() .
.
(1)求![]() 单调区间与极值;
单调区间与极值;
(2)当函数![]() 有两个极值点时,求实数
有两个极值点时,求实数![]() 的取值范围.
的取值范围.
【答案】(1)单调递增区间为![]() ;单调递减区间为
;单调递减区间为![]() ;
;![]() 极小值为
极小值为![]() ,不存在极大值;
,不存在极大值;
(2)![]()
【解析】
(1)首先求出函数的定义域、导函数,即可求出函数的单调区间与极值;
(2)首先求出导函数![]() ,由函数
,由函数![]() 有两个极值点,即等价于
有两个极值点,即等价于![]() 有两个解,即
有两个解,即![]() 有两个解,即求
有两个解,即求![]() 有两个解,结合(1)即可求出参数的取值范围;
有两个解,结合(1)即可求出参数的取值范围;
解:(1)依题意可知函数![]() 的定义域为
的定义域为![]()
![]()
当![]() 时,
时,![]() ,故函数
,故函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,故函数
,故函数![]() 在
在![]() 上单调递减;
上单调递减;
故函数![]() 在
在![]() 时取得极小值,即
时取得极小值,即![]() ,不存在极大值;
,不存在极大值;
综上所述,单调递增区间为![]() ;单调递减区间为
;单调递减区间为![]() ;
;![]() 极小值为
极小值为![]() ,不存在极大值;
,不存在极大值;
(2)因为![]() ,
,
所以![]()
求函数![]() 有两个极值点,又因为函数
有两个极值点,又因为函数![]() 是连续函数,等价于
是连续函数,等价于![]() 有两个解,即
有两个解,即![]() 有两个解,
有两个解,
由(1),可得求![]() 有两个解,即求
有两个解,即求![]() 有两个解,
有两个解,
又因为![]() ,且函数
,且函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
所以![]()
即![]()

【题目】某市大力推广纯电动汽车,对购买用户依照车辆出厂续驶里程R的行业标准,予以地方财政补贴.其补贴标准如下表:
出厂续驶里程R(公里) | 补贴(万元/辆) |
| 3 |
| 4 |
| 4.5 |
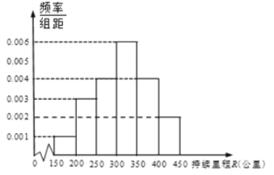
2019年底随机调查该市1000辆纯电动汽车,统计其出厂续驶里程R,得到频率分布直方图如上图所示用样本估计总体,频率估计概率,解决如下问题:
(1)求该市每辆纯电动汽车2019年地方财政补贴的均值;
(2)某企业统计2019年其充电站100天中各天充电车辆数,得如下的频数分布表:
辆数 |
|
|
|
|
天数 | 20 | 30 | 40 | 10 |
(同一组数据用该区间的中点值作代表)
2020年3月,国家出台政策,将纯电动汽车财政补贴逐步转移到充电基础设施建设上来该企业拟将转移补贴资金用于添置新型充电设备,现有直流、交流两种充电桩可供购置.直流充电桩5万元/台,每台每天最多可以充电30辆车,每天维护费用500元/台;交流充电桩1万元/台,每台每天最多可以充电4辆车,每天维护费用80元/台.该企业现有两种购置方案:
方案一:购买100台直流充电桩和900台交流充电桩;
方案二:购买200台直流充电桩和400台交流充电桩.
假设车辆充电时优先使用新设备,且充电一辆车产生25元的收入,用2019年的统计数据,分别估计该企业在两种方案下新设备产生的最大日利润.(日利润![]() 日收入
日收入![]() 日维护费用).
日维护费用).