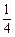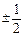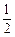题目内容
数列{an}中,a1=1,an+1=
-an+c(c>1为常数,n=1,2,3,…),且a3-a2=
.
(Ⅰ)求c的值;
(Ⅱ)①证明:an<an+1;
②猜测数列{an}是否有极限?如果有,写出极限的值(不必证明);
(Ⅲ)比较
与
an+1的大小,并加以证明.
| 1 |
| 2 |
| a | 2n |
| 1 |
| 8 |
(Ⅰ)求c的值;
(Ⅱ)①证明:an<an+1;
②猜测数列{an}是否有极限?如果有,写出极限的值(不必证明);
(Ⅲ)比较
| n |
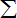 |
| k=1 |
| 1 |
| ak |
| 40 |
| 39 |
(Ⅰ)依题意,a2=
-a1+c=c-
,a3=
-a2+c=
(c-
)2+
.
由a3-a2=
,得
(c-
)2+
-(c-
)=
,
解得c=2,或c=1(舍去).
(Ⅱ)①证明:因为an+1-an=
-2an+2=
(an-2)2≥0,
当且仅当an=2时,an+1=an.
因为a1=1,所以an+1-an>0,即an<an+1(n=1,2,3,).
②数列{an}有极限,且
an=2.
(Ⅲ)由an+1=
-an+2,可得an(an+1-an)=(an-2)(an+1-2),
从而
=
-
.
因为a1=1,所以
=
(
-
)=
-
=
-1.
所以
-
an+1=
-1-
an+1=
=
.
因为a1=1,由(Ⅱ)①得an≥1(n∈N*).(1)
下面证明:对于任意n∈N*,有an<2成立.
当n=1时,由a1=1,显然结论成立.
假设结论对n=k(k≥1)时成立,即ak<2.
因为an+1=
-an+2=
(an-1)2+
,且函数y=
(x-1)2+
在x≥1时单调递增,
所以ak+1<
(2-1)2+
=2.
即当n=k+1时,结论也成立.于是,当n∈N*时,有an<2成立.(2)
根据(1)、(2)得1≤an<2.
由a1=1及an+1=
-an+2,经计算可得a2=
,a3=
.
所以,当n=1时,
<
a2;当n=2时,
+
=
a3;
当n≥3时,由
<an+1<2,得
-
an+1=
>0⇒
>
an+1.
| 1 |
| 2 |
| a | 21 |
| 1 |
| 2 |
| 1 |
| 2 |
| a | 22 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由a3-a2=
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
解得c=2,或c=1(舍去).
(Ⅱ)①证明:因为an+1-an=
| 1 |
| 2 |
| a | 2n |
| 1 |
| 2 |
当且仅当an=2时,an+1=an.
因为a1=1,所以an+1-an>0,即an<an+1(n=1,2,3,).
②数列{an}有极限,且
| lim |
| n→∞ |
(Ⅲ)由an+1=
| 1 |
| 2 |
| a | 2n |
从而
| 1 |
| an |
| 1 |
| an-2 |
| 1 |
| an+1-2 |
因为a1=1,所以
| n |
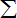 |
| k=1 |
| 1 |
| ak |
| n |
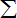 |
| k=1 |
| 1 |
| ak-2 |
| 1 |
| ak+1-2 |
| 1 |
| a1-2 |
| 1 |
| an+1-2 |
| 1 |
| 2-an+1 |
所以
| n |
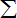 |
| k=1 |
| 1 |
| ak |
| 40 |
| 39 |
| 1 |
| 2-an+1 |
| 40 |
| 39 |
40
| ||
| 39•(2-an+1) |
| (5an+1+3)(8an+1-13) |
| 39•(2-an+1) |
因为a1=1,由(Ⅱ)①得an≥1(n∈N*).(1)
下面证明:对于任意n∈N*,有an<2成立.
当n=1时,由a1=1,显然结论成立.
假设结论对n=k(k≥1)时成立,即ak<2.
因为an+1=
| 1 |
| 2 |
| a | 2n |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
所以ak+1<
| 1 |
| 2 |
| 3 |
| 2 |
即当n=k+1时,结论也成立.于是,当n∈N*时,有an<2成立.(2)
根据(1)、(2)得1≤an<2.
由a1=1及an+1=
| 1 |
| 2 |
| a | 2n |
| 3 |
| 2 |
| 13 |
| 8 |
所以,当n=1时,
| 1 |
| a1 |
| 40 |
| 39 |
| 1 |
| a1 |
| 1 |
| a2 |
| 40 |
| 39 |
当n≥3时,由
| 13 |
| 8 |
| n |
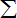 |
| k=1 |
| 1 |
| ak |
| 40 |
| 39 |
| (5an+1+3)(8an+1-13) |
| 39•(2-an+1) |
| n |
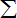 |
| k=1 |
| 1 |
| ak |
| 40 |
| 39 |

练习册系列答案
相关题目
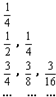
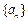 的各项为正,公比
的各项为正,公比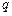 满足
满足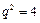 ,则
,则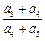 的值为()
的值为()