Question

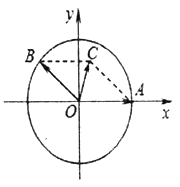
【题目】如图所示，在平面上，点，点在单位圆上且 .

（1）若点，求的值：

（2）若，四边形的面积用表示，求的取值范围.

Answer 1

【答案】（1）﹣，（2）．

【解析】

（1）根据三角函数的定义求得tanθ，进而得到tan2θ，最后求出．（2）由条件求出，于是得到+=sinθ+cosθ+1=sin（θ+）+1（0＜θ＜π），然后再根据三角函数的相关知识求解．

（1）由条件得B（﹣，），∠AOB=θ，

∴ tanθ==﹣，

∴ tan2θ = = = ，

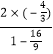∴tan（2θ+）= = =﹣．

（2）由题意得=||||sin（π﹣θ）=sinθ．

∵=（1，0），=（cosθ，sinθ），

∴ =+=（1+cosθ，sinθ），

∴ =1+cosθ，

∴ +=sinθ+cosθ+1=sin（θ+）+1（0＜θ＜π），

∵ ＜＜，

∴﹣＜sin（）≤1，

∴ ．

∴+的取值范围为．