��Ŀ����
5�� ��ϸ�ֹܺ��Ӷ��ɵĻ�̳Χ����������ͼ��ʾ�����������һ����������PQRS���ڲ���һ�������ߺ�һ�������������ߵĶ����������ϵ��е��Ǻ��ӵ�O�����ε����������������ϣ����������е������ε������������Լ������ĺ��ӵ�A��B���������������µ��������ӵ�ΪC��D����֪���εĸ���40���ף�C��D�����ľ���Ϊ40���ף�
��ϸ�ֹܺ��Ӷ��ɵĻ�̳Χ����������ͼ��ʾ�����������һ����������PQRS���ڲ���һ�������ߺ�һ�������������ߵĶ����������ϵ��е��Ǻ��ӵ�O�����ε����������������ϣ����������е������ε������������Լ������ĺ��ӵ�A��B���������������µ��������ӵ�ΪC��D����֪���εĸ���40���ף�C��D�����ľ���Ϊ40���ף���1�������AB�ij��ȣ�
��2���������������ϳ��ȣ�
��ע��ϸ�ֹܵĴ�ϸ�����غ��Բ��ƣ���������ȷ��1���ף���
���� ��1����OΪԭ�㣬���ε��ϵ�����ֱ��Ϊx�ᣬ����ֱ������ϵ���������µ���y�ύ�ڵ�M�������ߵķ���Ϊ��x2=2py��p��0��������D��20��-40�������p���õ������߷��̣�����������AB�ij��ȣ�
��2��˵�����������е������ε�����������Ψһ�Ĺ�������${l_{RQ}}��y+20=k��{x-10\sqrt{2}}����{k��0}��$���������������߷��̣�ͨ�����й�ϵ�����ֱ�ߵ�б�ʣ�Ȼ��������������������ϳ��ȣ�
���  �⣺��1����ͼ����OΪԭ�㣬���ε��ϵ�����ֱ��Ϊx�ᣬ����ֱ������ϵ��
�⣺��1����ͼ����OΪԭ�㣬���ε��ϵ�����ֱ��Ϊx�ᣬ����ֱ������ϵ��
�������µ���y�ύ�ڵ�M�������ߵķ���Ϊ��x2=2py��p��0����
������D��20��-40������p=-5��x2=-10y��3����
ȡ$y=-20⇒x=��10\sqrt{2}$��
��$A��{-10\sqrt{2}��-20}����B��{10\sqrt{2}��-20}��$��
$|{AB}|=20\sqrt{2}��28��{cm}��$
�𣺺���AB�ij���ԼΪ28cm����6��
��2�������⣬�����������е������ε�����������Ψһ�Ĺ�����
��${l_{RQ}}��y+20=k��{x-10\sqrt{2}}����{k��0}��$��7��
$\left\{{\begin{array}{l}{y+20=k��{x-10\sqrt{2}}��}\\{{x^2}=-10y}\end{array}}\right.⇒{x^2}+10kx-100��{2+\sqrt{2}k}��=0$��
��$��=100{k^2}+400��{2+\sqrt{2}k}��=0⇒k=-2\sqrt{2}$����${l_{RQ}}��y=-2\sqrt{2}x+20$��10��
��$Q��{5\sqrt{2}��0}����R��{15\sqrt{2}��-40}��$$⇒|{OQ}|=5\sqrt{2}��|{MR}|=15\sqrt{2}��|{RQ}|=30\sqrt{2}$��
�����ܳ�Ϊ$2��{5\sqrt{2}+15\sqrt{2}+30\sqrt{2}}��=100\sqrt{2}��141��{cm}��$��
�����������������ϳ���ԼΪ141cm��14��
���� ���⿼�������߷��̵�Ӧ�ã�ֱ���������ߵ�λ�ù�ϵ��Ӧ�ã�������������������������

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | $\frac{27}{2}$ | B�� | 6 | C�� | $\frac{9}{2}$ | D�� | $\frac{7}{2}$ |
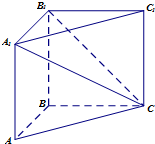 ��ͼ��ʾ����ֱ������ABC-A1B1C1�У�AB��BC��AB=BC=BB1����ƽ��A1B1C��ƽ��ABC���ɵĶ���ǵĴ�СΪ$\frac{��}{4}$��
��ͼ��ʾ����ֱ������ABC-A1B1C1�У�AB��BC��AB=BC=BB1����ƽ��A1B1C��ƽ��ABC���ɵĶ���ǵĴ�СΪ$\frac{��}{4}$�� | A�� | x1��x2 | B�� | x1��x2 | C�� | |x1|��|x2| | D�� | |x1|��|x2| |