题目内容
10.已知圆M:(x+$\sqrt{3}$)2+y2=16,点N($\sqrt{3}$,0),点P是圆上任意一点,线段NP的垂直平分线MP于点Q,设动点Q的轨迹为C(Ⅰ)求C的方程
(Ⅱ)设直线l:y=kx+m与轨迹C交于G,H两点,O为坐标原点,若△GOH的重心恰好在圆x2+y2=$\frac{4}{9}$上,求m的取值范围.
分析 (Ⅰ)如图,通过|QP|=|QN|,|MQ|+|QN|=|MP|=4,可知点Q的轨迹是以M、N为焦点,长轴长等于4的椭圆,即得椭圆C的方程;
(Ⅱ)设点G(x1,y1),H(x2,y2),联立直线l与椭圆C的方程,由韦达定理得x1+x2,从而可得y1+y2,及△GOH的重心的坐标并将其代入圆的方程,通过计算得${m}^{2}=\frac{(1+4{k}^{2})^{2}}{1+16{k}^{2}}$<1+4k2(k≠0),利用不等式即得实数m的取值范围.
解答  解:(Ⅰ)如图,∵|QP|=|QN|,∴|MQ|+|QN|=|MP|=4,
解:(Ⅰ)如图,∵|QP|=|QN|,∴|MQ|+|QN|=|MP|=4,
故点Q的轨迹是以M、N为焦点,长轴长等于4的椭圆,
所以椭圆C的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(Ⅱ)设点G(x1,y1),H(x2,y2),
方程联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$ 得,(1+4k2)x2+8kmx+4m2-4=0,
由韦达定理,得x1+x2=$-\frac{8mk}{1+4{k}^{2}}$,所以y1+y2=$\frac{2m}{1+4{k}^{2}}$,
所以△GOH的重心的坐标为($\frac{-8mk}{3(1+4{k}^{2})}$,$\frac{2m}{3(1+4{k}^{2})}$),
∴[$\frac{-8mk}{3(1+4{k}^{2})}$]2+[$\frac{2m}{3(1+4{k}^{2})}$]2=$\frac{4}{9}$,
整理得:${m}^{2}=\frac{(1+4{k}^{2})^{2}}{1+16{k}^{2}}$ ①
依题意△=(8mk)2-16(m2-1)(1+4k2)=16(1+4k2-m2)>0,得m2<1+4k2 ②
由①、②易得k≠0,
设t=1+16k2 (t>1),则$1+4{k}^{2}=\frac{t+3}{4}$,
所以m2=$\frac{t+\frac{9}{t}+6}{16}$$≥\frac{2\sqrt{t•\frac{9}{t}}+6}{16}$=$\frac{3}{4}$,当且仅当t=3取等号,
所以实数m的取值范围是$(-∞,-\frac{\sqrt{3}}{2}]∪[\frac{\sqrt{3}}{2},+∞)$.
点评 本题考查点的轨迹方程的求法,考查韦达定理、基本不等式、直线与圆的位置关系,解题时要认真审题,注意积累解题方法,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{6}$ | D. | 5 |
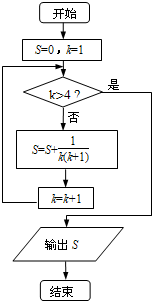
 定义运算a?b为执行如图所示的程序框图输出的S值,则(2cos$\frac{5π}{3}$)?(2tan$\frac{5π}{4}$)的值为4.
定义运算a?b为执行如图所示的程序框图输出的S值,则(2cos$\frac{5π}{3}$)?(2tan$\frac{5π}{4}$)的值为4.
 为了测算如图所示的阴影部分的面积,作一个边长为3的正方形将其包含在内,并向正方形内随机投掷600个点.已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是( )
为了测算如图所示的阴影部分的面积,作一个边长为3的正方形将其包含在内,并向正方形内随机投掷600个点.已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是( ) “十一黄金周”期间某市再次迎来了客流高峰,小李从该市的A地到B地有L1、L2两条路线(如图),L1路线上有A1、A2、A3三个路口,各路口遇到堵塞的概率均为$\frac{2}{3}$;L2路线上有B1、B2两个路口,各路口遇到堵塞的概率依次为$\frac{3}{4}$、$\frac{3}{5}$.
“十一黄金周”期间某市再次迎来了客流高峰,小李从该市的A地到B地有L1、L2两条路线(如图),L1路线上有A1、A2、A3三个路口,各路口遇到堵塞的概率均为$\frac{2}{3}$;L2路线上有B1、B2两个路口,各路口遇到堵塞的概率依次为$\frac{3}{4}$、$\frac{3}{5}$.