题目内容
已知n次多项式Sn(x)=(1+2x)(1+4x)(1+8x)…(1+2nx),其中n是正整数.记Sn(x)的展开式中x的系数是an,x2的系数是bn.
(Ⅰ)求an;
(Ⅱ)证明:bn+1-bn=4n+1-2n+2;
(Ⅲ)是否存在等比数列{cn}和正数c,使得bn=(cn-c)(cn+1-c)对任意正整数n成立?若存在,求出通项cn和正数c;若不存在,说明理由.
(Ⅰ)求an;
(Ⅱ)证明:bn+1-bn=4n+1-2n+2;
(Ⅲ)是否存在等比数列{cn}和正数c,使得bn=(cn-c)(cn+1-c)对任意正整数n成立?若存在,求出通项cn和正数c;若不存在,说明理由.
(Ⅰ)由题意得,an=2+4+…+2n,即an=
=2n+1-2.
(Ⅱ)证明:由Sn(x)=(1+2x)(1+4x)…(1+2nx),
得Sn+1(x)=(1+2n+1x)•Sn(x).
所以bn+1=bn+2n+1•an=bn+2n+2(2n-1),即bn+1-bn=2n+2(2n-1)=4n+1-2n+2.
(Ⅲ)由S1(x)=1+2x,得b1=0.
当n≥2时,
由bn=
(bk-bk-1)=
2k+1(2k-1-1)=4[
-
]=4(2-2n)(1-
),
得bn=
(2n-1-1)(2n-1).
当n=1时,b1=0也适合上式,故bn=
(2n-1-1)(2n-1),n∈N*.
因此,存在正数c=
=
和等比数列cn=c•2n-1=
•2n,使得bn=(cn-c)(cn+1-c)对于任意
正整数n成立.
| 2(1-2n) |
| 1-2 |
(Ⅱ)证明:由Sn(x)=(1+2x)(1+4x)…(1+2nx),
得Sn+1(x)=(1+2n+1x)•Sn(x).
所以bn+1=bn+2n+1•an=bn+2n+2(2n-1),即bn+1-bn=2n+2(2n-1)=4n+1-2n+2.
(Ⅲ)由S1(x)=1+2x,得b1=0.
当n≥2时,
由bn=
| n |
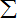 |
| k=2 |
| n |
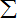 |
| k=2 |
| 22-22n |
| 1-4 |
| 2-2n |
| 1-2 |
| 2+2n |
| 3 |
得bn=
| 8 |
| 3 |
当n=1时,b1=0也适合上式,故bn=
| 8 |
| 3 |
因此,存在正数c=
|
2
| ||
| 3 |
| ||
| 3 |
正整数n成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 }中,
}中, ,且
,且
 ,
, 的值;
的值;