题目内容
20.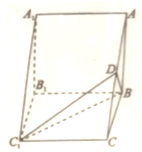 如图,三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB=BC,侧面A1B1BA和B1C1CB都是边长为2的正方形,D为AC的中点.
如图,三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB=BC,侧面A1B1BA和B1C1CB都是边长为2的正方形,D为AC的中点.(1)求证;AB1∥平面BDC1;
(2)求证:A1C⊥平面BDC1;
(3)求二面角B1-BC1-D的正弦值.
分析 (1)连接B1C交BC1于O,连接OD,然后由三角形的中位线的性质得到OD∥AB1,再由线面平行的判断得答案;
(2)在三棱柱ABC-A1B1C1中,由侧面A1B1BA和B1C1CB都是正方形,得到AA1⊥BD,再由AB=BC,D为AC的中点,可得BD⊥AC,进一步得到BD⊥A1C,由线面垂直的判断和性质得到A1C⊥BC1,又BD∩BC1=B,可得A1C⊥BDC1;
(3)以B1为坐标原点,以B1C1、B1B、B1A1所在直线分别为x、y、z轴建立空间直角坐标系,求出所用点的坐标,得到平面BC1D的一个法向量,找出平面BC1B1的一个法向量,由两法向量所成角的余弦值求得二面角B1-BC1-D的正弦值.
解答 (1)证明:连接B1C交BC1于O,连接OD,
在△CAB1中,由O、D分别是B1C和AC的中点,得OD∥AB1,
而AB1?平面BDC1,OD?平面BDC1,
∴AB1∥平面BDC1; (2)证明:三棱柱ABC-A1B1C1中,侧面A1B1BA和B1C1CB都是正方形,
(2)证明:三棱柱ABC-A1B1C1中,侧面A1B1BA和B1C1CB都是正方形,
∴BB1⊥平面ABC,AA1⊥平面ABC,而BD?平面ABC,
∴AA1⊥BD.
∵AB=BC=2,D为AC的中点,
∴BD⊥AC,BD⊥平面AA1C1C.
∴BD⊥A1C,
又A1B1⊥B1C1,A1B1⊥B1B,B1C1∩B1B=B1,
∴A1B1⊥平面B1C1CB,则A1B1⊥BC1.
在正方形B1C1CB中,B1C⊥BC1,A1B1∩B1C=B1,
∴BC1⊥平面A1B1C,而A1C?平面A1B1C,
∴A1C⊥BC1,又BD∩BC1=B,
∴A1C⊥BDC1;
(3)解: 以B1为坐标原点,以B1C1、B1B、B1A1所在直线分别为x、y、z轴建立空间直角坐标系,
以B1为坐标原点,以B1C1、B1B、B1A1所在直线分别为x、y、z轴建立空间直角坐标系,
则B(0,2,0),A(0,2,2),C1(2,0,0),C(2,2,0),D(1,2,1),
$\overrightarrow{{C}_{1}B}=(-2,2,0),\overrightarrow{BD}=(1,0,1)$,
设平面BC1D的一个法向量$\overrightarrow{{n}_{1}}=(x,y,z)$,
由$\overrightarrow{{n}_{1}}⊥\overrightarrow{{C}_{1}B},\overrightarrow{{n}_{1}}⊥\overrightarrow{BD}$,得$\left\{\begin{array}{l}{-2x+2y=0}\\{x+z=0}\end{array}\right.$,
令x=1,得$\overrightarrow{{n}_{1}}=(1,1,-1)$,
又平面BC1B1的一个法向量$\overrightarrow{{n}_{2}}=\overrightarrow{{B}_{1}{A}_{1}}=(0,0,1)$,
∴|cos<$\overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}}$>|=$\frac{|\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}|}{|\overrightarrow{{n}_{1}}|•|\overrightarrow{{n}_{2}}|}$=$\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$.
∴二面角B1-BC1-D的正弦值为$\frac{\sqrt{6}}{3}$.
点评 本题考查直线与平面平行、垂直的判断与性质,考查了学生的空间想象和思维能力,训练了利用空间向量求解二面角的平面角,是中档题.

(1)“?x∈R,2x+5>0”是全称命题;
(2)命题“?x∈R,x2+5x=6”的否定是“?x0∉R,使x02+5x0≠6”;
(3)若|x|=|y|,则x=y;
(4)若p∨q为假命题,则p、q均为假命题.
其中真命题的序号是( )
| A. | (1)(2) | B. | (2)(4) | C. | (1)(4) | D. | (1)(2)(3)(4) |
| A. | 4+3i | B. | 4-3i | C. | -3+4i | D. | -3-4i |
| A. | a、b、c三个实数中最多有一个不大于零 | |
| B. | a、b、c三个实数中最多有两个小于零 | |
| C. | a、b、c三个实数中至少有两个小于零 | |
| D. | a、b、c三个实数中至少有一个不大于零 |