题目内容
5.已知数列{an}是首项为1,公比为q的等比数列.(Ⅰ)证明:当0<q<1时,{an}是递减数列;
(Ⅱ)若对任意k∈N*,都有ak,ak+2,ak+1成等差数列,求q的值.
分析 (I)运用等比数列的通项公式,求得an,再由an+1-an,分解因式,结合条件即可得证;
(II)运用等差数列的性质和等比数列的通项公式,化简整理,计算即可得到q.
解答 (I)证明:因为数列{an}是首项为1,公比为q的等比数列,
所以an=qn-1,n∈N*.
所以an+1-an=qn-qn-1=qn-1(q-1),
当0<q<1时,有qn-1>0,q-1<0,
所以an+1-an<0,n∈N*.
所以{an}是递减数列.
(II)解:因为ak,ak+2,ak+1成等差数列,
所以2ak+2-(ak+ak+1)=0,其中k∈N*.
即2qk+1-(qk-1+qk)=0,
整理得qk-1•(2q2-q-1)=0.
因为q≠0,
所以2q2-q-1=0,
解得q=1,或q=$-\frac{1}{2}$.
点评 本题考查等差数列和等比数列的通项和性质,考查数列的单调性的证明,考查运算能力,属于中档题.

练习册系列答案
相关题目
15.三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,N是BC的中点,点P在A1B1上,且满足$\overrightarrow{{A_1}P}$=λ$\overrightarrow{{A_1}{B_1}}$,直线PN与平面ABC所成角θ的正切值取最大值时λ的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
16.已知点A(4,1,3),B(2,-5,1),C为线段AB上一点,且3|$\overrightarrow{AC}$|=|$\overrightarrow{AB}$|,则点C的坐标是( )
| A. | $(\frac{7}{2},-\frac{1}{2},\frac{5}{2})$ | B. | $(\frac{3}{8},-3,2)$ | C. | $(\frac{10}{3},-1,\frac{7}{3})$ | D. | $(\frac{5}{2},-\frac{7}{2},\frac{3}{2})$ |
10.如图阴影部分的面积是( )
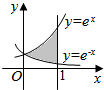

| A. | e+$\frac{1}{e}$ | B. | e+$\frac{1}{e}$-1 | C. | e+$\frac{1}{e}$-2 | D. | e-$\frac{1}{e}$ |
17.函数f(x)=x+2cosx在[0,π]上的极小值点为( )
| A. | 0 | B. | $\frac{π}{6}$ | C. | $\frac{5π}{6}$ | D. | π |
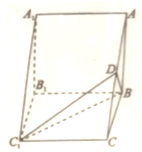 如图,三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB=BC,侧面A1B1BA和B1C1CB都是边长为2的正方形,D为AC的中点.
如图,三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB=BC,侧面A1B1BA和B1C1CB都是边长为2的正方形,D为AC的中点.