题目内容
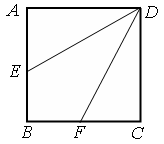
如图,边长为2的正方形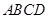 中,点
中,点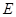 是
是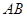 的中点,点
的中点,点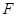 是
是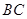 的中点,将△
的中点,将△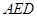 、△
、△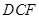 分别沿
分别沿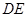 、
、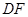 折起,使
折起,使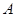 、
、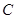 两点重合于点
两点重合于点 ,连接
,连接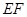 ,
,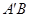 .
.
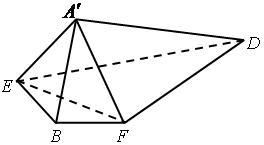
(1)求证: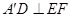 ;
;
(2)求二面角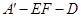 的余弦值.
的余弦值.
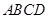 中,点
中,点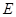 是
是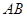 的中点,点
的中点,点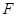 是
是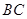 的中点,将△
的中点,将△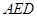 、△
、△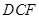 分别沿
分别沿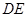 、
、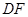 折起,使
折起,使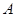 、
、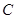 两点重合于点
两点重合于点 ,连接
,连接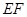 ,
,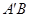 .
.

(1)求证:
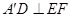 ;
;(2)求二面角
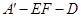 的余弦值.
的余弦值.(1)详见解析;(2) .
.
 .
.试题分析:(1)由
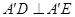 ,
,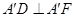 证出
证出 平面
平面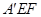 ,进而证出结论;(2)方法一:根据对称可判断
,进而证出结论;(2)方法一:根据对称可判断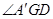 即为所求,由(1)可证△
即为所求,由(1)可证△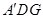 为直角三角形,再求出边长即可;方法二:建系,求出平面
为直角三角形,再求出边长即可;方法二:建系,求出平面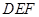 和平面
和平面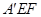 的法向量,两法向量的夹角的余弦值即为所求.
的法向量,两法向量的夹角的余弦值即为所求.试题解析:(1)在正方形
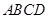 中,有
中,有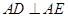 ,
,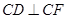 1分
1分则
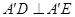 ,
,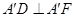 2分
2分又
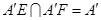 3分
3分∴
 平面
平面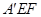 4分
4分而
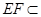 平面
平面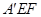 ,∴
,∴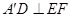 5分
5分(2)方法一:连接
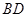 交
交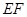 于点
于点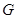 ,连接
,连接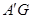 6分
6分∵在正方形
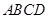 中,点
中,点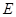 是
是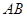 的中点,点
的中点,点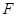 是
是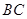 的中点,
的中点,∴
 ,
,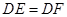 ,
,∴点
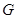 为
为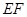 的中点,
的中点,且
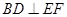 7分
7分∵正方形
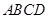 的边长为2,∴
的边长为2,∴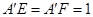 ,∴
,∴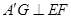 8分
8分∴
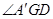 为二面角
为二面角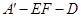 的平面角 9分
的平面角 9分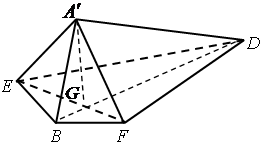
由(1)可得
 ,
,∴△
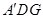 为直角三角形 10分
为直角三角形 10分∵正方形
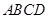 的边长为2,
的边长为2,∴
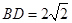 ,
,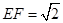 ,
,∴
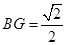 ,
,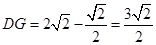 ,
,又
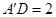 11分
11分∴
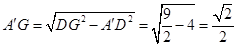 12分
12分∴
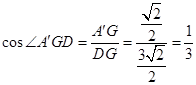 13分
13分∴二面角
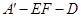 的余弦值为
的余弦值为 14分
14分方法二:∵正方形
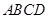 的边长为2,点
的边长为2,点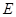 是
是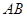 的中点,点
的中点,点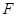 是
是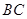 的中点,
的中点,∴
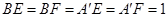 ,
,∴
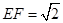 6分
6分∴
 ,∴
,∴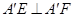 7分
7分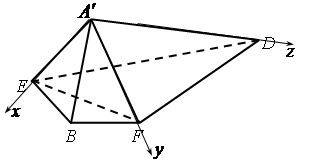
由(1)得
 平面
平面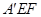 ,
,∴分别以
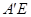 ,
, ,
,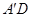 为
为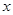 ,
,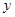 ,
,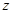 轴建立如图所示的空间直角
轴建立如图所示的空间直角坐标系
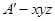 , 8分
, 8分则
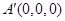 ,
,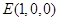 ,
,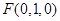 ,
,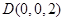 9分
9分∴
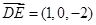 ,
,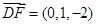 ,
,设平面
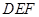 的一个法向量为
的一个法向量为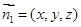 ,则由
,则由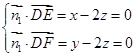 ,
,可取
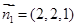 11分
11分又平面
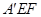 的一个法向量可取
的一个法向量可取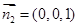 12分
12分∴
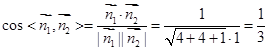 13分
13分∴二面角
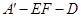 的余弦值为
的余弦值为 . 14分.
. 14分.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
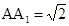 ,点E、F分别是面A1C1、面BC1的中心.
,点E、F分别是面A1C1、面BC1的中心.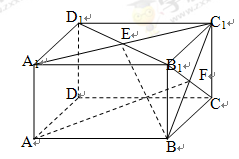
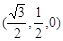 ,D点在平面yoz上,BC=2,∠BDC=90°,∠DCB=30°.
,D点在平面yoz上,BC=2,∠BDC=90°,∠DCB=30°.
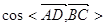 的值.
的值. =(1,5,-2),
=(1,5,-2),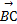 =(3,1,z),若
=(3,1,z),若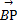 =(x-1,y,-3),且BP⊥平面ABC,则实数x,y,z分别为( )
=(x-1,y,-3),且BP⊥平面ABC,则实数x,y,z分别为( )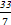 ,-
,-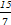 ,4
,4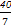 ,-
,-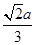 ,则MN与平面BB1C1C的位置关系是 ( ).
,则MN与平面BB1C1C的位置关系是 ( ).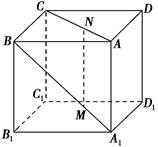
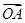 =
=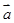 ,
,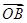 =
=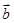 ,其中
,其中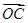 =λ
=λ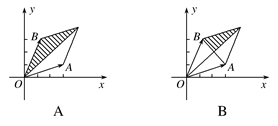
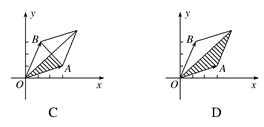
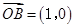 ,
,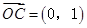 ,A为动点,
,A为动点,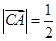 ,则
,则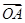 与
与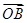 夹角的最小值为( )
夹角的最小值为( )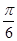
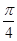
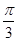
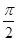
 等于( )
等于( )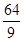
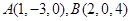 的距离是___________.
的距离是___________.