题目内容

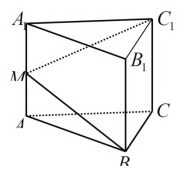
【题目】如图，在正三棱柱中，AB＝2，由顶点B沿棱柱侧面经过棱到顶点C1的最短路线与棱的交点记为M，求：

（Ⅰ）三棱柱的侧面展开图的对角线长.

（Ⅱ）该最短路线的长及的值.

（Ⅲ）平面与平面ABC所成二面角（锐二面角）

【答案】⑴；⑵,；⑶45°

【解析】

（Ⅰ）利用侧面展开法即可求出对角线长；

（Ⅱ）利用侧面展开法进行求解即可，求出DC1和的值即可；

（Ⅲ）连接DB，C1B，可证∠C1BC就是平面C1MB与平面ABC所成二面角的平面角，在三角形C1BC中求出此角的大小．

（Ⅰ）正三棱柱的侧面展开图是长为6， 宽为2的矩形，

其对角线长为

（Ⅱ）如图，将侧面绕棱AA1, , 旋转120°使其与侧面在同一平面上，点B运动到点D的位置，连接DC1交AA1于M，则DC1就是由顶点B沿棱柱侧面经过棱AA1到顶点C1的最短路线，其长为

,

故；

（Ⅲ）连接DB，C1B，则DB就是平面C1MB与平面ABC的交线，

在△DCB中，

,

,又平面

由三垂线定理得，

就是平面C1MB与平面ABC所成二面角的平面角（锐角），

∵侧面是正方形，，

故平面C1MB与平面ABC所成的二面角（锐角）为45°

练习册系列答案
相关题目

【题目】设圆的圆心在轴上，并且过两点.

(1)求圆的方程；

(2)设直线与圆交于两点，那么以为直径的圆能否经过原点，若能，请求出直线的方程；若不能，请说明理由.

【题目】某大学艺术专业400名学生参加某次测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成7组：[20，30），[30，40），…[80，90]，并整理得到如下频率分布直方图：

（Ⅰ）从总体的400名学生中随机抽取一人，估计其分数小于70的概率；
（Ⅱ）已知样本中分数小于40的学生有5人，试估计总体中分数在区间[40，50）内的人数；
（Ⅲ）已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等．试估计总体中男生和女生人数的比例．

【题目】如图，已知正四面体D﹣ABC（所有棱长均相等的三棱锥），P、Q、R分别为AB、BC、CA上的点，AP=PB， = =2，分别记二面角D﹣PR﹣Q，D﹣PQ﹣R，D﹣QR﹣P的平面角为α、β、γ，则（ ）

A.γ＜α＜β
B.α＜γ＜β
C.α＜β＜γ
D.β＜γ＜α

【题目】如图，已知四棱锥P﹣ABCD，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点．
（Ⅰ）证明：CE∥平面PAB；
（Ⅱ）求直线CE与平面PBC所成角的正弦值．

【题目】已知数列{xn}满足：x1=1，xn=xn+1+ln（1+xn+1）（n∈N*），证明：当n∈N*时，
（Ⅰ）0＜xn+1＜xn；
（Ⅱ）2xn+1﹣xn≤ ；
（Ⅲ） ≤xn≤ ．

【题目】在△ABC中，∠A=60°，c= a．（13分）
（1）求sinC的值；
（2）若a=7，求△ABC的面积．

【题目】如图，在三棱锥A﹣BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E、F（E与A、D不重合）分别在棱AD，BD上，且EF⊥AD． 求证：（Ⅰ）EF∥平面ABC；
（Ⅱ）AD⊥AC．

【题目】已知a＞0，b＞0，a3+b3=2，证明：
（Ⅰ）（a+b）（a5+b5）≥4；
（Ⅱ）a+b≤2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网