题目内容
【题目】如图,在直三棱柱ABC![]() 中,AC=3,BC=4,AB=5,A
中,AC=3,BC=4,AB=5,A![]() =4.
=4.
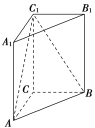
(1)证明:![]() ;
;
(2)求二面角![]() 的余弦值大小.
的余弦值大小.
【答案】⑴见证明;⑵![]()
【解析】
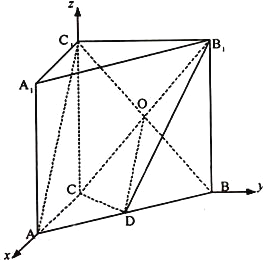
(1)根据AC,BC,CC1两两垂直,建立如图以C为坐标原点,建立空间直角坐标系C﹣xyz,写出要用的点的坐标,根据两个向量的数量级等于0,证出两条线段垂直.
(2)根据所给的两个平面的法向量一个可以直接看出另一个设出根据数量级等于0,求出结果,根据两个平面的法向量所成的角求出两个平面所成的角.
∵直三棱柱ABC﹣A1B1C1,底面三边长AC=3,BC=4,AB=5,
∴AC,BC,CC1两两垂直.
如图以C为坐标原点,建立空间直角坐标系C﹣xyz,则C(0,0,0),A(3,0,0),C1(0,0,4),B(0,4,0),B1(0,4,4). …(2分)
证明:(1)∵![]() =(﹣3,0,0),
=(﹣3,0,0),![]() =(0,﹣4,4),
=(0,﹣4,4),
∴![]()
![]() =0,
=0,
故AC⊥BC1…(4分)
解:(2)平面ABC的一个法向量为![]() =(0,0,1),
=(0,0,1),
设平面C1AB的一个法向量为![]() =(x,y,z),
=(x,y,z),
![]() =(﹣3,0,4),
=(﹣3,0,4),![]() =(﹣3,4,0),
=(﹣3,4,0),
由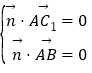 得:
得:![]() …(6分)
…(6分)
令x=4,则z=3,y=3则![]() =(4,3,3).…(7分)
=(4,3,3).…(7分)
故cos<![]() ,
,![]() >=
>=![]() =
=![]() .
.
即二面角![]() ABC的余弦值为
ABC的余弦值为![]() .
.

练习册系列答案
相关题目