题目内容
已知函数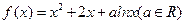 .
.
( 1)当
1)当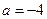 时,求
时,求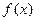 的最小值;
的最小值;
(2)若函数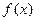 在区间
在区间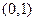 上为单
上为单 调函数,求实数
调函数,求实数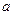 的取值范围;
的取值范围;
(3)当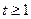 时,不等式
时,不等式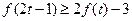 恒成立,求实数
恒成立,求实数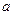 的取值范围.
的取值范围.
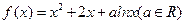 .
.(
 1)当
1)当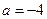 时,求
时,求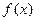 的最小值;
的最小值;(2)若函数
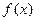 在区间
在区间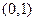 上为单
上为单 调函数,求实数
调函数,求实数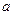 的取值范围;
的取值范围;(3)当
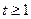 时,不等式
时,不等式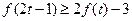 恒成立,求实数
恒成立,求实数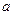 的取值范围.
的取值范围.解:(1) 当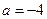 时,
时, 
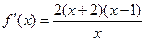
当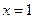 时 函数
时 函数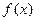 取最小值3.
取最小值3.
(2)
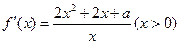 设
设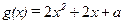
依题意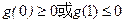 得
得 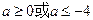 .
.
(3) 当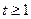 时
时 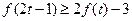 恒成立
恒成立
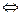 当
当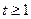 时
时 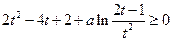 恒成立
恒成立
设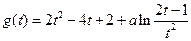 则
则
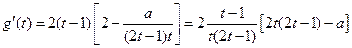
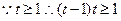
(1)当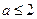 时,
时,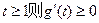
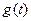 在
在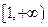 单调递增
单调递增
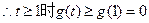
(2)当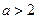 时,设
时,设
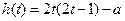
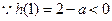
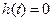 有两个根,一个根大于1,一个根小于1.
有两个根,一个根大于1,一个根小于1.
不妨设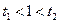
当
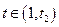 时
时 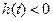 即
即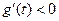
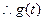
 在
在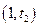 单调递减
单调递减 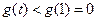
不满足已知条件.
综上: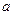 的取值范围为
的取值范围为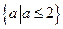 .
.
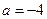 时,
时, 
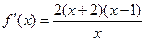
当
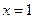 时 函数
时 函数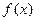 取最小值3.
取最小值3.(2)

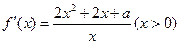 设
设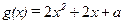
依题意
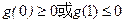 得
得 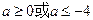 .
.(3) 当
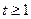 时
时 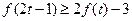 恒成立
恒成立 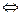 当
当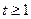 时
时 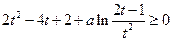 恒成立
恒成立设
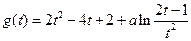 则
则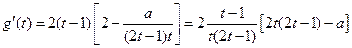
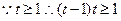
(1)当
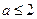 时,
时,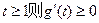
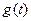 在
在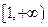 单调递增
单调递增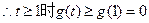
(2)当
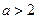 时,设
时,设
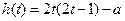
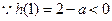
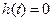 有两个根,一个根大于1,一个根小于1.
有两个根,一个根大于1,一个根小于1.不妨设
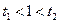
当

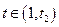 时
时 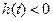 即
即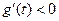
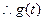
 在
在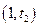 单调递减
单调递减 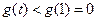
不满足已知条件.
综上:
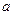 的取值范围为
的取值范围为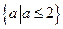 .
.略

练习册系列答案
相关题目
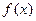 为定义在
为定义在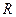 上的奇函数,且
上的奇函数,且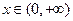 时,
时,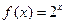
 的定义域;
的定义域;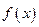 是定义在
是定义在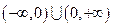 上的函数,且
上的函数,且
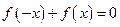 ,当
,当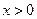 时,
时,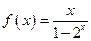 .
.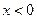 时,
时,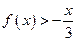
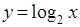
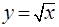
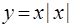
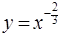
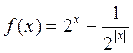
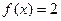 ,求
,求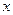 的值;
的值;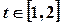 ,
,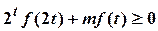 恒成立,求实数
恒成立,求实数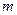 的取值范围。
的取值范围。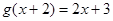 ,则
,则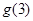 的值是 ( )
的值是 ( )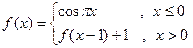 ,则
,则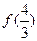 的值为_________
的值为_________ 取值范围是____________
取值范围是____________