题目内容
已知函数f(x)是偶函数,在(0,+¥)上导数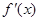 >0恒成立,则下列不等式成立的是
>0恒成立,则下列不等式成立的是
A f(-3)<f(-1)<f(2) B f(-1)<f(2)<f(-3)
C f(2)<f(-3)<f(-1) D f(2)<f(-1)<f(-3)
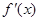 >0恒成立,则下列不等式成立的是
>0恒成立,则下列不等式成立的是A f(-3)<f(-1)<f(2) B f(-1)<f(2)<f(-3)
C f(2)<f(-3)<f(-1) D f(2)<f(-1)<f(-3)
B
f(x)是偶函数,则f(-x)= f(x),即f(-3)= f(3),f(-1)= f(1)。因为f(x)在(0,+¥)上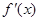 >0,即单调递增。所以f(1) <f(2)<f(3),则f(-1)<f(2)<f(-3)。
>0,即单调递增。所以f(1) <f(2)<f(3),则f(-1)<f(2)<f(-3)。
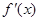 >0,即单调递增。所以f(1) <f(2)<f(3),则f(-1)<f(2)<f(-3)。
>0,即单调递增。所以f(1) <f(2)<f(3),则f(-1)<f(2)<f(-3)。
练习册系列答案
相关题目
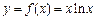 .
. 的图像在
的图像在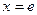 处的切线方程;
处的切线方程; ,求函数
,求函数 在
在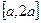 上的最大值
上的最大值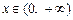 ,都有
,都有 成立.
成立.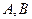 两地的距离是120km.假设汽油的价格是6元/升,以
两地的距离是120km.假设汽油的价格是6元/升,以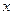 km/h(其中
km/h(其中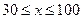 )速度行驶时,汽车的耗油率为
)速度行驶时,汽车的耗油率为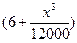 L/h,司机每小时的工资是28元.那么最经济的车速是多少?如不考虑其他费用,这次行车的总费用是多少?
L/h,司机每小时的工资是28元.那么最经济的车速是多少?如不考虑其他费用,这次行车的总费用是多少?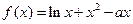 .
. 在其定义域上为增函数,求
在其定义域上为增函数,求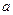 的取值范围;
的取值范围; (
(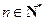 ),求证:
),求证: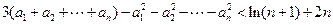 .
.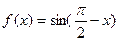 ,则要得到其导函数
,则要得到其导函数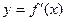 的图象,只需
的图象,只需 的图象 ( )
的图象 ( ) 个单位
个单位 个单位
个单位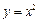 在点(1,1)处的切线的斜率为 .
在点(1,1)处的切线的斜率为 . ;若
;若 ..
..