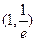题目内容
已知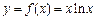 .
.
(1)求函数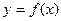 的图像在
的图像在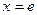 处的切线方程;
处的切线方程;
(2)设实数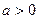 ,求函数
,求函数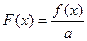 在
在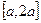 上的最大值
上的最大值
(3)证明对一切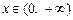 ,都有
,都有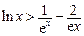 成立.
成立.
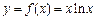 .
.(1)求函数
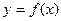 的图像在
的图像在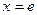 处的切线方程;
处的切线方程;(2)设实数
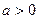 ,求函数
,求函数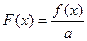 在
在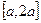 上的最大值
上的最大值(3)证明对一切
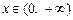 ,都有
,都有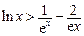 成立.
成立.(1)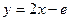 (2)
(2) 
 (3)同解析
(3)同解析
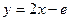 (2)
(2) 
 (3)同解析
(3)同解析(1) 定义域为
定义域为
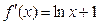
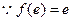 又
又 
 函数
函数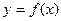 的在
的在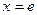 处的切线方程为:
处的切线方程为: ,即
,即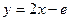
(2) 令
令 得
得 当
当 ,
, ,
, 单调递减,
单调递减,
当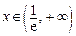 ,
,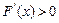 ,
, 单调递增.
单调递增.

 在
在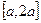 上的最大值
上的最大值
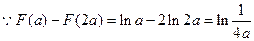
 当
当 时,
时,


当 时,
时, ,
,

(3)问题等价于证明 , 由(2)可知
, 由(2)可知 的最小值是
的最小值是 ,当且仅当
,当且仅当 时取得. 设
时取得. 设 ,则
,则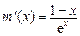 ,易得
,易得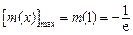 ,
,
当且仅当 时取到,从而对一切
时取到,从而对一切 ,都有
,都有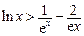 成立.
成立.
 定义域为
定义域为
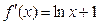
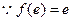 又
又 
 函数
函数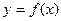 的在
的在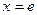 处的切线方程为:
处的切线方程为: ,即
,即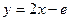
(2)
 令
令 得
得 当
当 ,
, ,
, 单调递减,
单调递减,当
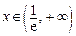 ,
,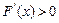 ,
, 单调递增.
单调递增. 
 在
在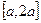 上的最大值
上的最大值
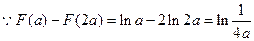
 当
当 时,
时,


当
 时,
时, ,
,

(3)问题等价于证明
 , 由(2)可知
, 由(2)可知 的最小值是
的最小值是 ,当且仅当
,当且仅当 时取得. 设
时取得. 设 ,则
,则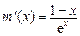 ,易得
,易得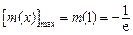 ,
,当且仅当
 时取到,从而对一切
时取到,从而对一切 ,都有
,都有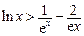 成立.
成立.
练习册系列答案
相关题目
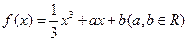 在
在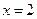 处取到极小值
处取到极小值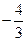 .
.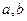 的值及函数
的值及函数 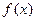 的单调区间;
的单调区间;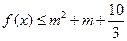 对
对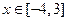 恒成立,求实数
恒成立,求实数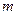 的取值范围.
的取值范围. (万元)与投入资金
(万元)与投入资金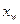 (万元)成正比例关系,又估计当投入资金6万元时,可获利润1.2万元.生产R型产品所获利润
(万元)成正比例关系,又估计当投入资金6万元时,可获利润1.2万元.生产R型产品所获利润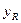 (万元)与投入资金
(万元)与投入资金 (万元)的关系满足
(万元)的关系满足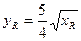 ,为获得最大利润,问生产W.R型两种产品各应投入资金多少万元?获得的最大利润是多少?(精确到0.01万元)
,为获得最大利润,问生产W.R型两种产品各应投入资金多少万元?获得的最大利润是多少?(精确到0.01万元) 
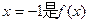 的一个极值点。求
的一个极值点。求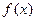 在区间
在区间 上的最大值和最小值;
上的最大值和最小值; 上不是单调函数,求
上不是单调函数,求 的取值范围。
的取值范围。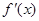 >0恒成立,则下列不等式成立的是
>0恒成立,则下列不等式成立的是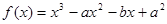 在
在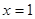 处有极值10, 则点
处有极值10, 则点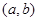 为( )
为( )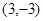
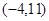

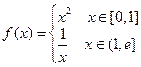 (其中
(其中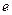 为自然对数的底数),则
为自然对数的底数),则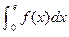 的值为
的值为 



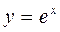 在点P处的切线斜率为e,则点P的坐标为( )
在点P处的切线斜率为e,则点P的坐标为( )