题目内容
曲线 与直线
与直线 有两个交点,则
有两个交点,则 的取值范围为( )
的取值范围为( )
A. | B.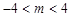 |
C. | D.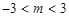 |
A
解析试题分析:画出 及y=2x的图象,当
及y=2x的图象,当 过(-2,0)时,m=4;当
过(-2,0)时,m=4;当 过(2,0)时,m=-4;观察知,
过(2,0)时,m=-4;观察知, 时,曲线
时,曲线 与直线
与直线 有两个交点,关系A。
有两个交点,关系A。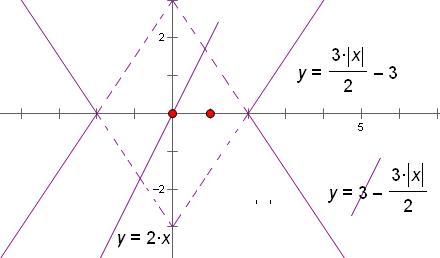
考点:本题考查两条直线的交点问题,
点评:基础题,涉及绝对值函数的图形分析,根据已知题意画出图形,然后根据数形结合分析m的取值范围.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
已知点P是双曲线 右支上一点,
右支上一点, 分别是双曲线的左、右焦点,I为
分别是双曲线的左、右焦点,I为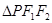 的内心,若
的内心,若  成立,则双曲线的离心率为( )
成立,则双曲线的离心率为( )
| A.4 | B. | C.2 | D. |
已知椭圆的中心在原点,焦点在x轴上,焦距等于6,离心率等于 ,则此椭圆的方程是
,则此椭圆的方程是
A. | B. |
C. | D. |
双曲线的离心率为 ,则双曲线的两条渐近线的夹角是
,则双曲线的两条渐近线的夹角是
| A.45° | B.30° | C.60° | D.90° |
已知抛物线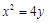 的焦点
的焦点 和点
和点 为抛物线上一点,则
为抛物线上一点,则 的最小值是( )
的最小值是( )
| A.3 | B.9 | C.12 | D.6 |
双曲线 的焦点坐标是 ( )
的焦点坐标是 ( )
| A.(–2,0),(2,0) | B.(0,–2),(0,2) |
| C.(0,–4),(0,4) | D.(–4,0),(4,0) |
若抛物线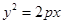 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )
| A.-2 | B.2 | C.-4 | D.4 |
与椭圆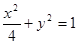 共焦点且过点
共焦点且过点 的双曲线方程是( )
的双曲线方程是( )
A.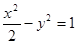 | B.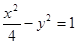 |
C. | D. |
 分别是双曲线
分别是双曲线 的左、右焦点,过
的左、右焦点,过 且垂直于
且垂直于 轴的直线与双曲线交于
轴的直线与双曲线交于 两点,若
两点,若 是钝角三角形,则该双曲线离心率的取值范围是
是钝角三角形,则该双曲线离心率的取值范围是


