题目内容
与椭圆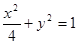 共焦点且过点
共焦点且过点 的双曲线方程是( )
的双曲线方程是( )
A.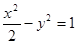 | B.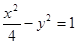 |
C. | D. |
A
解析试题分析:与椭圆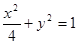 共焦点,说明焦点在
共焦点,说明焦点在 轴上,焦点为
轴上,焦点为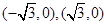 ,根据双曲线的定义知
,根据双曲线的定义知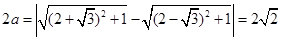 ,所以
,所以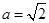 ,所以
,所以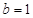 ,所以双曲线方程为
,所以双曲线方程为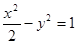
考点:本小题主要考查椭圆与双曲线的关系以及双曲线标准方程的求解,考查学生的运算求解能力.
点评:本小题也可以用待定系数法求解.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
曲线 与直线
与直线 有两个交点,则
有两个交点,则 的取值范围为( )
的取值范围为( )
A. | B.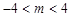 |
C. | D.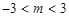 |
以 为中心,
为中心, ,
, 为两个焦点的椭圆上存在一点
为两个焦点的椭圆上存在一点 ,满足
,满足 ,则该椭圆的离心率为
,则该椭圆的离心率为
A.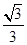 | B. | C. | D. |
已知 是椭圆
是椭圆 上的一动点,且
上的一动点,且 与椭圆长轴两顶点连线的斜率之积最小值为
与椭圆长轴两顶点连线的斜率之积最小值为 ,则椭圆离心率为
,则椭圆离心率为
A. | B. | C. | D. |
抛物线 的焦点坐标为( )
的焦点坐标为( )
A. | B.(1,0) | C.(0,- ) ) | D.(- ,0) ,0) |
已知点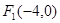 和
和 ,曲线上的动点P到
,曲线上的动点P到 、
、 的距离之差为6,则曲线方程为()
的距离之差为6,则曲线方程为()
A. | B.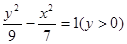 |
C. 或 或 | D. |
经过点 且与双曲线
且与双曲线 有共同渐近线的双曲线方程为( )
有共同渐近线的双曲线方程为( )
A. | B. |
C. | D. |
双曲线 的焦点坐标是( )
的焦点坐标是( )
A. | B. | C. | D. |
双曲线两条渐近线互相垂直,那么它的离心率为 ( )
| A.2 | B.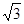 | C.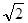 | D.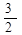 |