题目内容
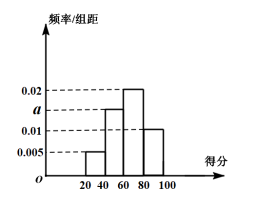
【题目】某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下:
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 | a | 24 | b |
(1)由该题中频率分布直方图求测试成绩的平均数和中位数;
(2)其他条件不变在评定等级为“合格”的学生中依次抽取2人进行座谈,每次抽取1人,求在第1次抽取的测试得分低于80分的前提下,第2次抽取的测试得分仍低于80分的概率;
(3)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中抽取10人进行座谈.现再从这10人中任选4人,记所选4人的量化总分为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
【答案】(1)64,65;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先求出![]() 的值,再利用频率分布直方图平均数和中位数的公式求解;
的值,再利用频率分布直方图平均数和中位数的公式求解;
(2)“第1次抽取的测试得分低于80分”为事件A,“第2次抽取的测试得分低于80分”为事件B,再利用条件概率求解;
(3)由题意可得![]() 的所有可能取值为0,5,10,15,20,再求出其对应的概率,即得
的所有可能取值为0,5,10,15,20,再求出其对应的概率,即得![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
由题意知,样本容量为![]() ,
,![]() ,
,
![]() ,
,![]() .
.
(1)平均数为![]() ,
,
设中位数为x,
因为![]()
![]() ,
,![]() ,
,
所以![]() ,则
,则![]() ,
,
解得![]() .
.
(2)由题意可知,分数在![]() 内的学生有24人,分数在
内的学生有24人,分数在![]() 内的学生有12人.设“第1次抽取的测试得分低于80分”为事件A,“第2次抽取的测试得分低于80分”为事件B,
内的学生有12人.设“第1次抽取的测试得分低于80分”为事件A,“第2次抽取的测试得分低于80分”为事件B,
则![]() ,
,![]() ,所以
,所以![]() .
.
(3)在评定等级为“合格”和“不合格”的学生中用分层抽样的方法抽取10人,则“不合格”的学生人数为![]() ,“合格”的学生人数为
,“合格”的学生人数为![]() .
.
由题意可得![]() 的所有可能取值为0,5,10,15,20
的所有可能取值为0,5,10,15,20
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
所以![]() 的分布列为
的分布列为
| 0 | 5 | 10 | 15 | 20 |
P |
|
|
|
|
|
![]() .
.

【题目】新生儿某疾病要接种三次疫苗免疫(即0、1、6月龄),假设每次接种之间互不影响,每人每次接种成功的概率相等为了解新生儿该疾病疫苗接种剂量与接种成功之间的关系,现进行了两种接种方案的临床试验:10μg/次剂量组与20μg/次剂量组,试验结果如下:
接种成功 | 接种不成功 | 总计(人) | |
10μg/次剂量组 | 900 | 100 | 1000 |
20μg/次剂量组 | 973 | 27 | 1000 |
总计(人) | 1873 | 127 | 2000 |
(1)根据数据说明哪种方案接种效果好?并判断能否有99.9%的把握认为该疾病疫苗接种成功与两种接种方案有关?
(2)以频率代替概率,若选用接种效果好的方案,参与该试验的1000人的成功人数比此剂量只接种一次的成功人数平均提高多少人.
参考公式: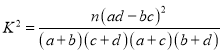 ,其中
,其中![]()
参考附表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |