题目内容
(本题满分12分)
已知函数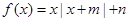 ,其中
,其中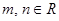
(1) 若 为R上的奇函数,求
为R上的奇函数,求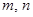 的值;
的值;
(2) 若常数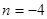 ,且
,且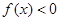 对任意
对任意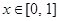 恒成立,求
恒成立,求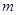 的取值范围.
的取值范围.
(Ⅰ)  (Ⅱ)
(Ⅱ) .
.
解析

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
题目内容
(本题满分12分)
已知函数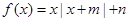 ,其中
,其中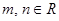
(1) 若 为R上的奇函数,求
为R上的奇函数,求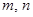 的值;
的值;
(2) 若常数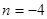 ,且
,且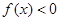 对任意
对任意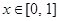 恒成立,求
恒成立,求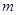 的取值范围.
的取值范围.
(Ⅰ)  (Ⅱ)
(Ⅱ) .
.
解析

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案