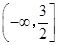题目内容
已知函数f(x)=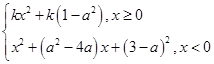 ,其中a∈R.若对任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立,则实数k的取值范围是________.
,其中a∈R.若对任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立,则实数k的取值范围是________.
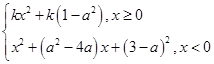 ,其中a∈R.若对任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立,则实数k的取值范围是________.
,其中a∈R.若对任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立,则实数k的取值范围是________.(-∞,0]∪[8,+∞)
由题知当x=0时,f(x)=k(1-a2).又对任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立,所以函数f(x)必须是连续函数,即在x=0附近的左、右两侧,其函数值相等.于是(3-a)2=k(1-a2),即(k+1)a2-6a+9-k=0有实数解,所以Δ=62-4(k+1)(9-k)≥0,解得k≤0或k≥8.

练习册系列答案
相关题目
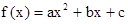 满足:
满足: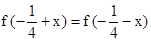 ,且
,且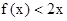 的
的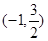
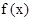 的解析式;
的解析式;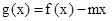
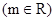 ,若
,若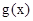 在
在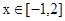 上的最小值为-4,求
上的最小值为-4,求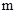 的值.
的值.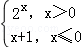 .若f(a)+f(1)=0,则实数a的值等于( )
.若f(a)+f(1)=0,则实数a的值等于( ) 的二次项系数为
的二次项系数为 ,且不等式
,且不等式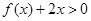 的解集为(1,3).
的解集为(1,3).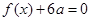 有两个相等实数根,求
有两个相等实数根,求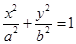 (a>b>0)的离心率为
(a>b>0)的离心率为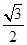 ,过其右焦点F与长轴垂直的弦长为1,
,过其右焦点F与长轴垂直的弦长为1,