题目内容
【题目】已知抛物线C:y2=4x,过焦点F作与x轴垂直的直线l1 , C上任意一点P(x0 , y0)(y0≠0)处的切线为l,l与l1交于M,l与准线交于N,则 ![]() = .
= .
【答案】1
【解析】解:抛物线C:y2=4x的焦点为F(1,0),准线为l:x=﹣1, 抛物线y2=4x两边对x求导,可得2yy′=4,即y′= ![]() ,
,
过P(x0 , y0)(y0≠0)的切线为l的斜率为 ![]() ,切线的方程为y﹣y0=
,切线的方程为y﹣y0= ![]() (x﹣x0),
(x﹣x0),
又y02=4x0 , 即有y0y=2(x+x0),
令x=﹣1,可得N(﹣1, ![]() ),
),
∴ ![]() =(1﹣x0 , ﹣y0),
=(1﹣x0 , ﹣y0), ![]() =(﹣2,
=(﹣2, ![]() ),
),
∴ ![]()
![]() =﹣2(1﹣x0)﹣y0
=﹣2(1﹣x0)﹣y0 ![]() =0,
=0,
∴ ![]() ⊥
⊥ ![]() ,
,
过P做PQ垂直于x=﹣1,交x=﹣1于Q,
由椭圆的定义可知:丨PQ丨=丨QF丨,
∴△NPQ≌△NPF,
∴∠PNQ=∠PNF,
∵∠PNQ=∠NMF,
∴∠PNF=∠NMF,
∴MF=NF,![]() =1,
=1,
所以答案是:1.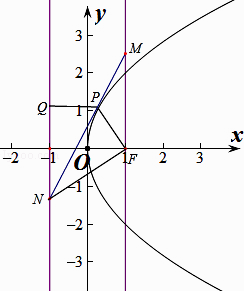

练习册系列答案
相关题目