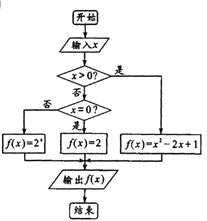
题目内容
【题目】已知直线![]() 与圆C:
与圆C:![]() 相交,截得的弦长为
相交,截得的弦长为![]() .
.
(1)求圆C的方程;
(2)过原点O作圆C的两条切线,与函数![]() 的图象相交于M、N两点(异于原点),证明:直线
的图象相交于M、N两点(异于原点),证明:直线![]() 与圆C相切;
与圆C相切;
(3)若函数![]() 图象上任意三个不同的点P、Q、R,且满足直线
图象上任意三个不同的点P、Q、R,且满足直线![]() 和
和![]() 都与圆C相切,判断线
都与圆C相切,判断线![]() 与圆C的位置关系,并加以证明.
与圆C的位置关系,并加以证明.
【答案】(1)![]() (2)证明见解析;(3)直线
(2)证明见解析;(3)直线![]() 与圆C相切;证明见解析;
与圆C相切;证明见解析;
【解析】
(1)化圆方程为标准方程,得圆心坐标和半径,求出圆心到直线的距离,用表示出弦长,从而求得![]() ,得圆方程;
,得圆方程;
(2)求出过原点的圆![]() 的两条切线方程,然后求得两条切线与抛物线的交点坐标后可得证;
的两条切线方程,然后求得两条切线与抛物线的交点坐标后可得证;
(3)设![]() ,
,![]() ,
,![]() ,由此写出直线
,由此写出直线![]() 的方程,由直线
的方程,由直线![]() 与圆相切得出
与圆相切得出![]() 的关系,可得
的关系,可得![]() ;
;![]() ,然后可证直线
,然后可证直线![]() 也与圆相切.
也与圆相切.
(1)解:圆C:![]() ,可化为圆
,可化为圆![]() ,
,
圆心到直线的距离![]() ,
,
∵截得的弦长为![]() ,
,
∴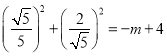 ,
,
∴![]() ,
,
∴圆C的方程为![]() ;
;
(2)证明:设过原点O的切线方程为![]() ,即
,即![]() ,
,
圆心到直线的距离![]() ,∴
,∴![]() ,
,
∴设过原点O的切线方程为![]() ,
,
与函数![]() ,联立可得
,联立可得![]() ,∴
,∴![]() 与圆C相切;
与圆C相切;
(3)解:设![]() ,
,![]() ,
,![]() ,可得
,可得![]() ,
,
直线![]() 的方程为
的方程为![]() ,即为
,即为![]() ,
,
同理可得,直线![]() 的方程为
的方程为![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
∵直线![]() 和
和![]() 都与圆C相切,
都与圆C相切,
∴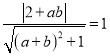 ,
,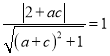 ,即为
,即为![]() ,
,
![]() ,即有b,c为方程
,即有b,c为方程![]() 的两根,
的两根,
可得![]() ;
;![]() ,
,
由圆心到直线![]() 的距离为
的距离为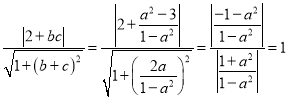 ,
,
则直线![]() 与圆C相切.
与圆C相切.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目