题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆上.
在椭圆上.
(1)求椭圆的方程;
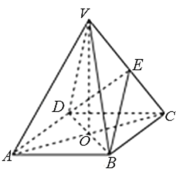
(2)过椭圆的右焦点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() 、
、![]() ,其中直线
,其中直线![]() 交椭圆于
交椭圆于![]() 两点,直线
两点,直线![]() 交直线
交直线![]() 于
于![]() 点,求证:直线
点,求证:直线![]() 平分线段
平分线段![]() .
.
【答案】(1) ![]() (2)见证明
(2)见证明
【解析】
(1)利用![]() ,得到
,得到![]() ,然后代入点
,然后代入点![]() 即可求解
即可求解
(2)设直线,以斜率![]() 为核心参数,与椭圆联立方程,把
为核心参数,与椭圆联立方程,把![]() 两点全部用参数
两点全部用参数![]() 表示,得出
表示,得出![]() 的中点坐标为
的中点坐标为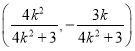 ,然后再求出直线
,然后再求出直线![]() 的方程,代入
的方程,代入![]() 的中点即可证明成立
的中点即可证明成立
(1)由![]() 得
得![]() ,所以
,所以![]()
由点![]() 在椭圆上得
在椭圆上得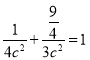 解得
解得![]() ,
,
![]()
所求椭圆方程为![]()
(2)解法一:当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 平分线段
平分线段![]() 成立
成立
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 方程为
方程为![]() ,
,
联立方程得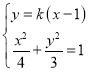 ,消去
,消去![]() 得
得![]()
因为![]() 过焦点,所以
过焦点,所以![]() 恒成立,设
恒成立,设![]() ,
,![]() ,
,
则![]() ,
,![]()
![]()
所以![]() 的中点坐标为
的中点坐标为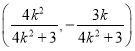
直线![]() 方程为
方程为![]() ,
,![]() ,可得
,可得![]() ,
,
所以直线![]() 方程为
方程为![]() ,
,
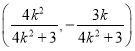 满足直线
满足直线![]() 方程,即
方程,即![]() 平分线段
平分线段![]()
综上所述,直线![]() 平分线段
平分线段![]()
(2)解法二:因为直线![]() 与
与![]() 有交点,所以直线
有交点,所以直线![]() 的斜率不能为0,
的斜率不能为0,
可设直线![]() 方程为
方程为![]() ,
,
联立方程得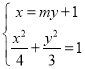 ,消去
,消去![]() 得
得![]()
因为![]() 过焦点,所以
过焦点,所以![]() 恒成立,设
恒成立,设![]() ,
,![]() ,
,
![]() ,
,![]()
![]()
所以![]() 的中点坐标为
的中点坐标为![]()
直线![]() 方程为
方程为![]() ,
,![]() ,由题可得
,由题可得![]() ,
,
所以直线![]() 方程为
方程为![]() ,
,
![]() 满足直线
满足直线![]() 方程,即
方程,即![]() 平分线段
平分线段![]()
综上所述,直线![]() 平分线段
平分线段![]()

【题目】工厂质检员从生产线上每半个小时抽取一件产品并对其某个质量指标![]() 进行检测,一共抽取了
进行检测,一共抽取了![]() 件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标
件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标![]() 有关,具体见下表.
有关,具体见下表.
质量指标 |
|
|
|
频数 |
|
|
|
一年内所需维护次数 |
|
|
|
(1)以每个区间的中点值作为每组指标的代表,用上述样本数据估计该厂产品的质量指标![]() 的平均值(保留两位小数);
的平均值(保留两位小数);
(2)用分层抽样的方法从上述样本中先抽取![]() 件产品,再从
件产品,再从![]() 件产品中随机抽取
件产品中随机抽取![]() 件产品,求这
件产品,求这![]() 件产品的指标
件产品的指标![]() 都在
都在内的概率;
(3)已知该厂产品的维护费用为![]() 元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加
元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加![]() 元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这
元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这![]() 件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?