题目内容
17.已知f(x)=x+sinx,若x∈[1,2]时,f(x2-ax)+f(1-x)≤0,则a的取值范围是( )| A. | a≤1 | B. | a≥1 | C. | a≥$\frac{3}{2}$ | D. | a≤$\frac{3}{2}$ |
分析 求出函数的导数,判断函数的单调性,推出函数的奇偶性,即可转化不等式为二次不等式恒成立,即可求出a的范围.
解答 解:因为f(x)=sinx+x,x∈R,
而f(-x)=sin(-x)+(-x)=-sinx-x=-f(x),
所以函数的奇函数;
又f′(x)=cosx+1≥0,所以函数是增函数,
若x∈[1,2]时,f(x2-ax)+f(1-x)≤0,
f(x2-ax)≤-f(1-x)=f(x-1),
所以x2-ax≤x-1在x∈[1,2]恒成立,
即有1-a-1+1≤0且4-2a-2+1≤0,
即有a≥1且a≥$\frac{3}{2}$,
则a≥$\frac{3}{2}$.
故选C.
点评 本题考查函数的单调性、奇偶性的判断与应用,考查不等式恒成立问题的解决方法,属于中档题.

练习册系列答案
相关题目
9.数列{an}满足an+an+1=$\frac{1}{2}$(n∈N,n≥1),若a2=1,Sn是{an}的前n项和,则S21的值为( )
| A. | -$\frac{1}{2}$ | B. | 1 | C. | $\frac{9}{2}$ | D. | -$\frac{9}{2}$ |
7.下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( )
| A. | y=cos2x,x∈R | B. | y=x3+1,x∈R | ||
| C. | y=$\frac{{e}^{x}-{e}^{-x}}{2}$,x∈R | D. | y=log2|x|,x∈R且x≠0 |
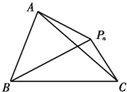 如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3:1,$\overrightarrow{{P_n}A}$=$\frac{{{x_{n+1}}}}{3}$$\overrightarrow{{P_n}B}$-(2xn+1)$\overrightarrow{{P_n}C}$(其中,{xn}是首项为1的正项数列),则x4等于( )
如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3:1,$\overrightarrow{{P_n}A}$=$\frac{{{x_{n+1}}}}{3}$$\overrightarrow{{P_n}B}$-(2xn+1)$\overrightarrow{{P_n}C}$(其中,{xn}是首项为1的正项数列),则x4等于( )