题目内容
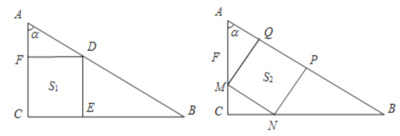
【题目】正方形![]() 和
和![]() 内接于同一个直角三角形ABC中,如图所示,设
内接于同一个直角三角形ABC中,如图所示,设![]() ,若两正方形面积分别为
,若两正方形面积分别为![]() =441,
=441,![]() =440,则
=440,则![]() =______
=______
【答案】![]()
【解析】
首先根据在正方形S1和S2内,S1=441,S2=440,分别求出两个正方形的边长,然后分别表示出AF、FC、AM、MC的长度,最后根据AF+FC=AM+MC,列出关于α的三角函数等式,求出sin2α的值即可.
因为S1=441,S2=440,
所以FD![]() 21,MQ=MN
21,MQ=MN![]() ,
,
因为AC=AF+FC![]() 21
21![]() 21,
21,
AC=AM+MC![]() MNcosα
MNcosα![]() cosα,
cosα,
所以:![]() 21
21![]() cosα,
cosα,
整理,可得:![]() (sinαcosα+1)=21(sinα+cosα),
(sinαcosα+1)=21(sinα+cosα),
两边平方,可得110sin22α﹣sin2α﹣1=0,
解得sin2α![]() 或sin2α
或sin2α![]() (舍去),
(舍去),
故sin2α![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目
