题目内容
【题目】已知函数f(x)=sin(x﹣ ![]() )+cos(x﹣
)+cos(x﹣ ![]() ),g(x)=2sin2
),g(x)=2sin2 ![]() .
.
(1)若α是第一象限角,且f(α)= ![]() ,求g(α)的值;
,求g(α)的值;
(2)求使f(x)≥g(x)成立的x的取值集合.
【答案】
(1)解:∵f(x)= ![]() sinx﹣
sinx﹣ ![]() cosx+
cosx+ ![]() cosx+
cosx+ ![]() sinx=
sinx= ![]() sinx,
sinx,
所以f(α)= ![]() sinα=
sinα= ![]() ,所以sinα=
,所以sinα= ![]() .
.
又α∈(0, ![]() ),所以cosα=
),所以cosα= ![]() ,
,
所以g(α)=2sin2 ![]() =1﹣cosα=
=1﹣cosα= ![]() .
.
(2)解:由f(x)≥g(x)得 ![]() sinx≥1﹣cosx,
sinx≥1﹣cosx,
所以 ![]() sinx+
sinx+ ![]() cosx=sin(x+
cosx=sin(x+ ![]() )≥
)≥ ![]() .
.
解2kπ+ ![]() ≤x+
≤x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈z,求得2kπ≤x≤2kπ+
,k∈z,求得2kπ≤x≤2kπ+ ![]() ,k∈z,
,k∈z,
所以x的取值范围为〔2kπ,2kπ+ ![]() 〕k∈z.
〕k∈z.
【解析】(1)利用两角和差的三角公式化简函数f(x)的解析式,可得f(α)的解析式,再根据f(α)= ![]() ,求得cosα的值,从而求得g(α)=2sin2
,求得cosα的值,从而求得g(α)=2sin2 ![]() =1﹣cosα的值.(2)由不等式可得 sin(x+
=1﹣cosα的值.(2)由不等式可得 sin(x+ ![]() )≥
)≥ ![]() ,解不等式 2kπ+
,解不等式 2kπ+ ![]() ≤x+
≤x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈z,求得x的取值集合.
,k∈z,求得x的取值集合.
【考点精析】掌握两角和与差的正弦公式和二倍角的余弦公式是解答本题的根本,需要知道两角和与差的正弦公式:![]() ;二倍角的余弦公式:
;二倍角的余弦公式:![]() .
.

【题目】( 2013湖南)某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示: 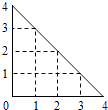
X | 1 | 2 | 3 | 4 |
Y | 51 | 48 | 45 | 42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰 好“相近”的概率;
(2)在所种作物中随机选取一株,求它的年收获量的分布列与数学期望.