题目内容
设P(x,y)是圆(x-2)2+y2=1上任意一点,则(x-5)2+(y+4)2的最大值为 .
考点:圆的标准方程
专题:计算题,直线与圆
分析:运用圆的参数方程,设P(2+cosα,sinα),代入化简整理,再由两角差的正弦公式,结合正弦函数的值域,即可得到最大值.
解答:
解:由于P(x,y)是圆(x-2)2+y2=1上任意一点,
设P(2+cosα,sinα),
则(x-5)2+(y+4)2=(cosα-3)2+(4+sinα)2
=cos2α-6cosα+9+16+8sinα+sin2α=8sinα-6cosα+26
=10(
sinα-
cosα)+26=10sin(α-θ)+26(θ为辅助角)
当sin(α-θ)=1,取得最大值,且为36.
故答案为:36.
设P(2+cosα,sinα),
则(x-5)2+(y+4)2=(cosα-3)2+(4+sinα)2
=cos2α-6cosα+9+16+8sinα+sin2α=8sinα-6cosα+26
=10(
| 4 |
| 5 |
| 3 |
| 5 |
当sin(α-θ)=1,取得最大值,且为36.
故答案为:36.
点评:本题考查圆的参数方程的运用:求最值,考查三角函数的化简和求值,考查运算能力,属于中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
已知sin(3π+α)=lg
,则tan(π+α)的值是( )
| 1 | |||
|
A、-
| ||||
B、
| ||||
C、±
| ||||
D、
|
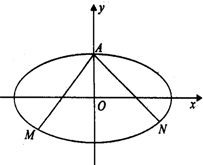 如图已知椭圆
如图已知椭圆