题目内容
 已知椭圆C1的中心在坐标原点,焦点在x轴上,且经过点P(
已知椭圆C1的中心在坐标原点,焦点在x轴上,且经过点P(| 2 |
| ||
| 2 |
(1)求椭圆C1的标准方程;
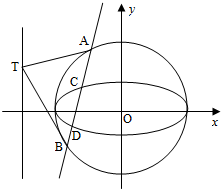
(2)如图,以椭圆C1的长轴为直径作圆C2,过直线x=-2上的动点T作圆C2的两条切线,设切点分别为A、B,若直线AB与椭圆C1求交于不同的两点C、D,求
| |AB| |
| |CD| |
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知得
,由此能求出椭圆的标准方程.
(2)圆C2的方程为x2+y2=2,设直线x=-2上的动点T的坐标为(-2,t),(t∈R),设A(x1,y1),B(x2,y2),则直线AT的方程为x1x+y1y=2,直线BT的方程为x2x+y2y=2,直线AB的方程为-2x+ty=2,由此利用点到直线的距离和导数的性质能求出
的取值范围.
|
(2)圆C2的方程为x2+y2=2,设直线x=-2上的动点T的坐标为(-2,t),(t∈R),设A(x1,y1),B(x2,y2),则直线AT的方程为x1x+y1y=2,直线BT的方程为x2x+y2y=2,直线AB的方程为-2x+ty=2,由此利用点到直线的距离和导数的性质能求出
| |AB| |
| |CD| |
解答:
解:(1)设椭圆C1的标准方程为
+
=1(a>b>0),
将点P(
,0),Q(-1,-
)代入,得:
,解得a=
,b=1,
∴椭圆的标准方程为
+y2=1.
(2)圆C2的方程为x2+y2=2,
设直线x=-2上的动点T的坐标为(-2,t),(t∈R),
设A(x1,y1),B(x2,y2),则直线AT的方程为x1x+y1y=2,
直线BT的方程为x2x+y2y=2,
又T(-2,t)在直线AT和BT上,即
,
∴直线AB的方程为-2x+ty=2,
由原点O到直线AT的距离为d=
,
得|AB|=2
=2
,
联立
,消去x,得(t2+8)y2-4ty-4=0,
设C(x3,y3),D(x4,y4),
则y3+y4=
,y3y4=
,
从而|CD|=
|y1-y2|=
,
∴
=
,
设t2+4=m,m>4,
则
=
=
,
又设
=s.0<s≤
,
则
=
,
设f(s)=1+6s-32s3,
令f′(s)=6-96s2=0,解得s=
,
故f(s)=1+6s-32s3在s∈(0,
]上单调递增,
f(s)∈(1,2],
∴
∈(1,
].
| x2 |
| a2 |
| y2 |
| b2 |
将点P(
| 2 |
| ||
| 2 |
|
| 2 |
∴椭圆的标准方程为
| x2 |
| 2 |
(2)圆C2的方程为x2+y2=2,
设直线x=-2上的动点T的坐标为(-2,t),(t∈R),
设A(x1,y1),B(x2,y2),则直线AT的方程为x1x+y1y=2,
直线BT的方程为x2x+y2y=2,
又T(-2,t)在直线AT和BT上,即
|
∴直线AB的方程为-2x+ty=2,
由原点O到直线AT的距离为d=
| 2 | ||
|
得|AB|=2
| r2-d2 |
|
联立
|
设C(x3,y3),D(x4,y4),
则y3+y4=
| 4t |
| t2+8 |
| -4 |
| t2+8 |
从而|CD|=
1+
|
2
| ||||
| t2+8 |
∴
| |AB| |
| |CD| |
(t2+8)
| ||
(t2+4)
|
设t2+4=m,m>4,
则
| |AB| |
| |CD| |
|
1+
|
又设
| 1 |
| m |
| 1 |
| 4 |
则
| |AB| |
| |CD| |
| 1+6s-32s2 |
设f(s)=1+6s-32s3,
令f′(s)=6-96s2=0,解得s=
| 1 |
| 4 |
故f(s)=1+6s-32s3在s∈(0,
| 1 |
| 4 |
f(s)∈(1,2],
∴
| |AB| |
| |CD| |
| 2 |
点评:本题考查椭圆的方程的求法,考查两线段比值的取值范围的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
若0<x<
,0<y<
,且sinx=xcosy,则( )
| π |
| 2 |
| π |
| 2 |
A、y<
| ||||
B、
| ||||
C、
| ||||
| D、x<y |
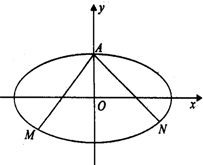 如图已知椭圆
如图已知椭圆