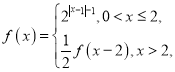题目内容
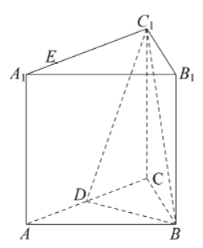
【题目】已知矩形![]() 中,
中,![]() ,E,F分别为
,E,F分别为![]() ,
,![]() 的中点.沿
的中点.沿![]() 将矩形
将矩形![]() 折起,使
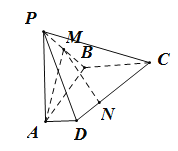
折起,使![]() ,如图所示.设P、Q分别为线段
,如图所示.设P、Q分别为线段![]() ,
,![]() 的中点,连接
的中点,连接![]() .
.
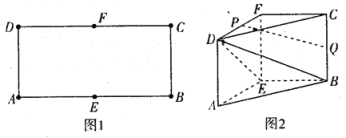
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1) 取![]() 中点R,连接
中点R,连接![]() ,
,![]() ,可知
,可知![]() 中,
中,![]() 且
且![]() ,由Q是
,由Q是![]() 中点,可得则有
中点,可得则有![]() 且
且![]() ,即四边形
,即四边形![]() 是平行四边形,则有
是平行四边形,则有![]() ,即证得
,即证得![]() 平面
平面![]() .
.
(2) 建立空间直角坐标系,求得半平面的法向量: ![]() ,
,![]() 然后利用空间向量的相关结论可求得二面角
然后利用空间向量的相关结论可求得二面角![]() 的余弦值.
的余弦值.
(1)取![]() 中点R,连接
中点R,连接![]() ,
,![]() ,
,
则在![]() 中,
中,![]() ,且
,且![]() ,
,
又Q是![]() 中点,所以
中点,所以![]() ,
,
而且![]() ,所以
,所以![]() ,
,
所以四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)在平面![]() 内作
内作![]() 交
交![]() 于点G,以E为原点,
于点G,以E为原点,![]() ,
,![]() ,
,![]() 分别为x,y,x轴,
分别为x,y,x轴,
建立如图所示的空间直角坐标系,
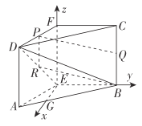
则各点坐标为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则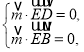 即
即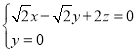 ,
,
取![]() ,得
,得![]() ,
,
又平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以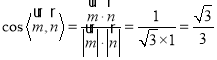 .
.
因此,二面角![]() 的余弦值为
的余弦值为![]()

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案【题目】某省确定从2021年开始,高考采用“![]() ”的模式,取消文理分科,即“3”包括语文、数学、外语,为必考科目;“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取
”的模式,取消文理分科,即“3”包括语文、数学、外语,为必考科目;“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中含男生110人,求
名学生中含男生110人,求![]() 的值及抽取到的女生人数;
的值及抽取到的女生人数;
(2)学校计划在高二上学期开设选修中的“物理”和“历史”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生进行问卷调杳(假定每名学生在这两个科目中必须洗择一个科目且只能选择一个科目).下表是根据调查结果得到的
名学生进行问卷调杳(假定每名学生在这两个科目中必须洗择一个科目且只能选择一个科目).下表是根据调查结果得到的![]() 列联表,请将列联表补充完整,并判断是否有
列联表,请将列联表补充完整,并判断是否有![]() 的把握认为选择科目与性别有关?说明你的理由;
的把握认为选择科目与性别有关?说明你的理由;
性别 | 选择物理 | 选择历史 | 总计 |
男生 | 50 | ||
女生 | 30 | ||
总计 |
(3)在(2)的条件下,从抽取的选择“物理”的学生中按分层抽样抽取6人,再从这6名学生中抽取2人,对“物理”的选课意向作深入了解,求2人中至少有1名女生的概率.
附: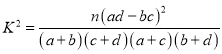 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |