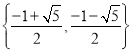题目内容
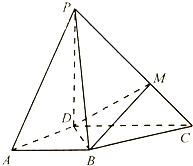
【题目】如图，在四棱锥P-ABCD中，底面ABCD为正方形，平面PAD⊥底面ABCD，PD⊥AD，PD=AD，E为棱PC的中点
（I）证明：平面PBC⊥平面PCD；
（II）求直线DE与平面PAC所成角的正弦值；
（III）若F为AD的中点，在棱PB上是否存在点M，使得FM⊥BD？若存在，求
的值，若不存在，说明理由．
【答案】（Ⅰ）见解析（II）
（III）存在，
=
【解析】
（I）由面面垂直的性质定理得PD⊥底面ABCD，从而可得BC⊥平面PCD，然后可证得面面垂直；
（II）以
为
轴建立空间直角坐标系，写出各点坐标，求出平面的法向量和直线的方向向量，平面的法向量和直线的方向向量的余弦的绝对值等于直线与平面所成角的正弦；
（III）设
=λ
（0≤λ≤1），由
求得
即可．
（I）∵平面PAD⊥底面ABCD，又PD⊥AD，
∴PD⊥底面ABCD
∴PD⊥BC
又∵底面ABCD为正方形，BC⊥CD
∴BC⊥平面PCD
∴平面PBC⊥平面PCD，
（II）由（I）知，PD⊥底面ABCD，AD⊥CD
如图以点D为原点建立空间直角坐标系
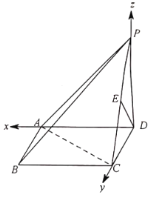
不妨设PD=AD=2，可得D（0，0，0），A（2，0，0，），C（0，2，0），P（0，0，2），
由E为棱PC的中点，得E（0，1，1），
向量
=（-2，2，0），
=（2，0，-2），设
=(x,y,z)为平面PAC的法向量，则
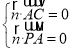，即
不妨令x=1,可得=（1，1，1）为平面PAC的一个法向量
设直线DE与平面PAC所成角为θ
所以sinθ=
=
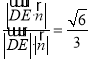
所以，直线DE与平面PAC所成角的正弦值为
（III）向量=（-2，-2，2），
=（2，2，0），
=（1，2，0）
由点M在棱PB上，设=λ（0≤λ≤1）
故
=+=（1-2λ，2-2λ，2λ）
由FM⊥DB，得·=0
因此（1-2λ）×2+（2-2λ）×2=0
解得λ=
，所以
=
