题目内容
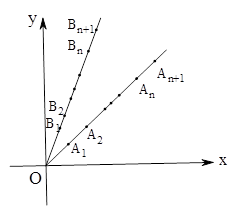
(本题满分18分)如图,平面直角坐标系中,射线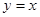 (
(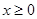 )和
)和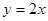 (
(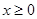 )上分别依次有点
)上分别依次有点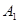 、
、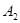 ,……,
,……,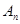 ,……,和点
,……,和点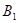 ,
,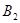 ,……,
,……,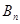 ……,其中
……,其中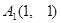 ,
,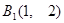 ,
,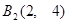 .且
.且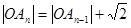 ,
, 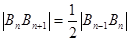
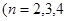 ……).
……).
(1)用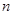 表示
表示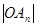 及点
及点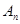 的坐标;
的坐标;
(2)用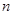 表示
表示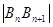 及点
及点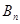 的坐标;
的坐标;
(3)写出四边形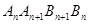 的面积关于
的面积关于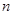 的表达式
的表达式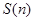 ,并求
,并求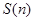 的最大值.
的最大值.
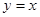 (
(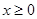 )和
)和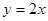 (
(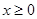 )上分别依次有点
)上分别依次有点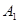 、
、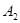 ,……,
,……,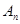 ,……,和点
,……,和点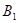 ,
,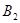 ,……,
,……,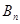 ……,其中
……,其中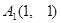 ,
,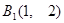 ,
,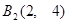 .且
.且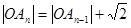 ,
, 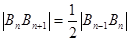
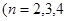 ……).
……).(1)用
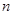 表示
表示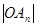 及点
及点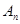 的坐标;
的坐标;(2)用
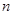 表示
表示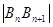 及点
及点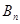 的坐标;
的坐标;(3)写出四边形
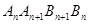 的面积关于
的面积关于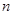 的表达式
的表达式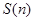 ,并求
,并求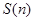 的最大值.
的最大值.
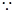
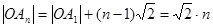 ……………2分
……………2分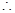
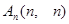 …………4分
…………4分(2)
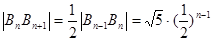 …………7分
…………7分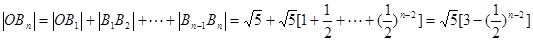
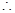
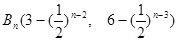 …………10分
…………10分(3)
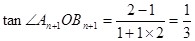 ,
,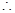
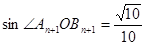 …………12分
…………12分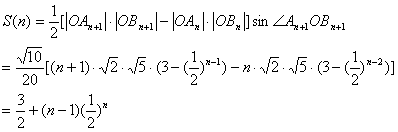 ………15分
………15分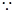
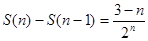 ,
,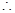
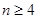 时,
时,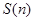 单调递减.
单调递减.又
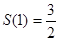 ,
,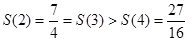 .
.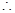
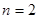 或
或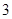 时,
时,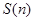 取得最大值
取得最大值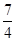 …………18分
…………18分(1)由题意得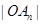 组成一个等差数列,根据等差数列的通项公式得
组成一个等差数列,根据等差数列的通项公式得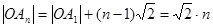 ,
,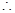
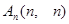
(2)由题意得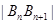 组成一个等比数列,
组成一个等比数列,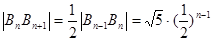 ,所以
,所以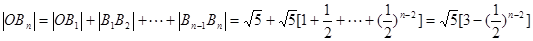
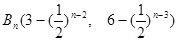
(3)四边形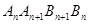 的面积等于
的面积等于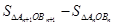 ,由题意和三角函数的公式可得
,由题意和三角函数的公式可得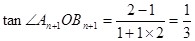 ,
,
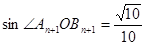 根据三角形的面积公式求出两个三角形的面积得四边形的面积,研究其单调性得最大值。
根据三角形的面积公式求出两个三角形的面积得四边形的面积,研究其单调性得最大值。
解:
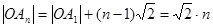 ……………2分
……………2分
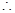
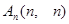 …………4分
…………4分
(2)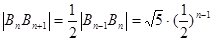 …………7分
…………7分
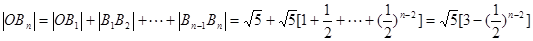
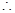
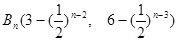 …………10分
…………10分
(3)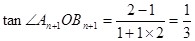 ,
,
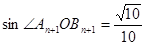 …………12分
…………12分
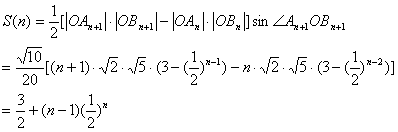 ………15分
………15分
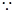
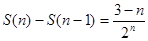 ,
,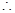
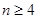 时,
时,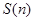 单调递减.
单调递减.
又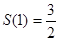 ,
,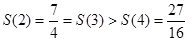 .
.
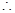
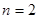 或
或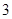 时,
时,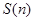 取得最大值
取得最大值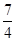 …………18分
…………18分
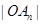 组成一个等差数列,根据等差数列的通项公式得
组成一个等差数列,根据等差数列的通项公式得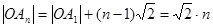 ,
,
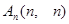
(2)由题意得
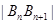 组成一个等比数列,
组成一个等比数列,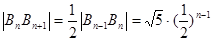 ,所以
,所以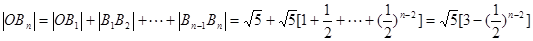
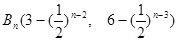
(3)四边形
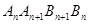 的面积等于
的面积等于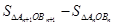 ,由题意和三角函数的公式可得
,由题意和三角函数的公式可得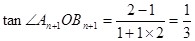 ,
,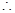
 根据三角形的面积公式求出两个三角形的面积得四边形的面积,研究其单调性得最大值。
根据三角形的面积公式求出两个三角形的面积得四边形的面积,研究其单调性得最大值。解:
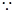
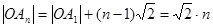 ……………2分
……………2分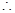
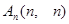 …………4分
…………4分(2)
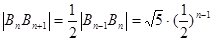 …………7分
…………7分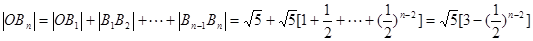
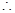
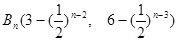 …………10分
…………10分(3)
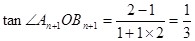 ,
,
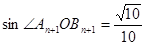 …………12分
…………12分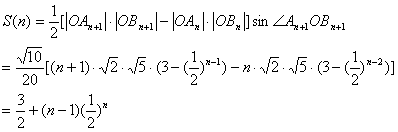 ………15分
………15分
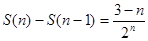 ,
,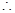
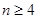 时,
时,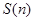 单调递减.
单调递减.又
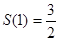 ,
,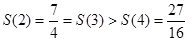 .
.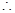
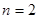 或
或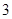 时,
时,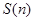 取得最大值
取得最大值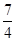 …………18分
…………18分
练习册系列答案
相关题目
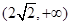
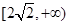
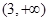
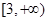
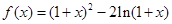 .
.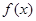 的单调区间;
的单调区间;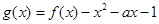 在区间
在区间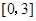 上的最小值.
上的最小值. .
.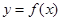 在点
在点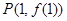 处的切线与直线
处的切线与直线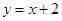 垂直,求函数
垂直,求函数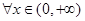 都有
都有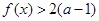 成立,试求
成立,试求 的取值范围;
的取值范围;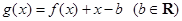 .当
.当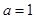 时,函数
时,函数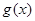 在区间
在区间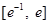 上有两个零点,求实数
上有两个零点,求实数 的取值范围.
的取值范围.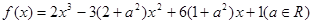
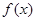 在
在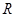 上单调,求
上单调,求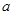 的值;
的值;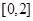 上的最大值是
上的最大值是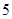 ,求
,求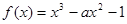 在
在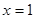 处的切线经过原点
处的切线经过原点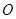 ,则函数
,则函数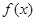 的极小值为 ▲
的极小值为 ▲  ,
, ,
,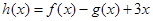 ,其中
,其中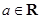 且
且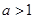 .
.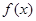 的导函数
的导函数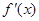 的最小值;
的最小值;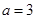 时,求函数
时,求函数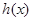 的单调区间及极值;
的单调区间及极值;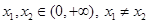 ,函数
,函数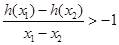 ,求实数
,求实数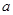 的取值范围.
的取值范围.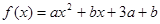 是偶函数,其定义域是
是偶函数,其定义域是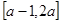 ,则
,则 在区间
在区间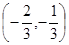 是减函数。
是减函数。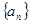 的前n项和
的前n项和 则此数列是等比数列的充要条件是
则此数列是等比数列的充要条件是
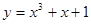 过点(1,3)处的切线方程为:
过点(1,3)处的切线方程为: 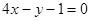 。
。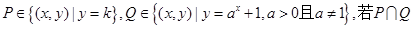 只有一个子集。则
只有一个子集。则
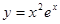 的单调递减区间是. ( )
的单调递减区间是. ( )