题目内容
函数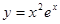 的单调递减区间是. ( )
的单调递减区间是. ( )
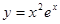 的单调递减区间是. ( )
的单调递减区间是. ( )| A.(–1, 2) | B.(–∞, –1)与(1, +∞) |
| C.(–∞, –2)与(0, +∞) | D.(–2,0) |
D
解:因为
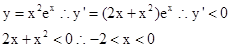
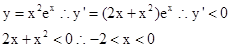

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
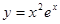 的单调递减区间是. ( )
的单调递减区间是. ( )| A.(–1, 2) | B.(–∞, –1)与(1, +∞) |
| C.(–∞, –2)与(0, +∞) | D.(–2,0) |
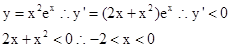

 阅读快车系列答案
阅读快车系列答案