题目内容
已知函数 ,
, ,
,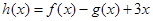 ,其中
,其中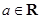 且
且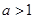 .
.
(I)求函数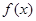 的导函数
的导函数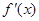 的最小值;
的最小值;
(II)当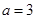 时,求函数
时,求函数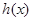 的单调区间及极值;
的单调区间及极值;
(III)若对任意的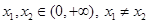 ,函数
,函数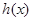 满足
满足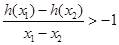 ,求实数
,求实数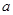 的取值范围.
的取值范围.
 ,
, ,
,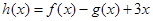 ,其中
,其中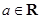 且
且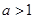 .
.(I)求函数
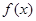 的导函数
的导函数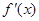 的最小值;
的最小值;(II)当
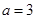 时,求函数
时,求函数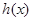 的单调区间及极值;
的单调区间及极值;(III)若对任意的
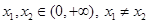 ,函数
,函数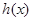 满足
满足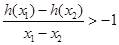 ,求实数
,求实数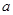 的取值范围.
的取值范围.解:(I)
 ,其中
,其中 .
.因为
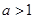 ,所以
,所以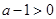 ,又
,又 ,所以
,所以 ,
,当且仅当
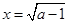 时取等号,其最小值为
时取等号,其最小值为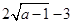 . ……………………………4分
. ……………………………4分(II)当
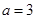 时,
时,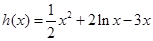 ,
, .
.………………………………………………………..6分
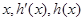 的变化如下表:
的变化如下表: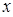 |  |  | 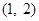 | 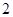 |  |
 |  | 0 |  | 0 |  |
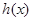 |  | 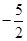 |  | 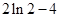 |  |
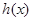 的单调增区间是
的单调增区间是 ,
, ;单调减区间是
;单调减区间是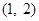 .
.函数
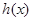 在
在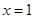 处取得极大值
处取得极大值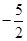 ,在
,在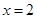 处取得极小值
处取得极小值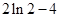 .
.(III)由题意,
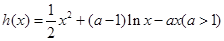 .
.不妨设
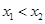 ,则由
,则由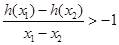 得
得 . ……………12分
. ……………12分令
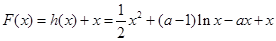 ,则函数
,则函数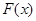 在
在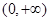 单调递增.
单调递增.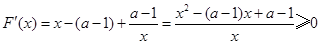 在
在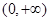 恒成立.
恒成立.即
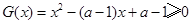 在
在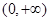 恒成立.
恒成立.因为
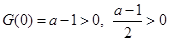 ,因此,只需
,因此,只需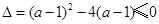 .
.解得
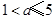 .
. 故所求实数
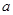 的取值范围为
的取值范围为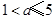
本试题主要考查了导数在研究函数中的运用。

练习册系列答案
相关题目
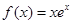 ,则( )
,则( ) 为
为 的极大值点
的极大值点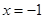 为
为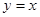 (
(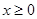 )和
)和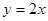 (
(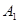 、
、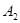 ,……,
,……,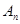 ,……,和点
,……,和点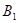 ,
,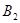 ,……,
,……,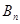 ……,其中
……,其中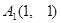 ,
,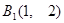 ,
,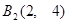 .且
.且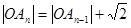 ,
, 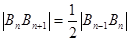
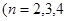 ……).
……).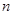 表示
表示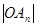 及点
及点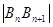 及点
及点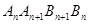 的面积关于
的面积关于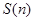 ,并求
,并求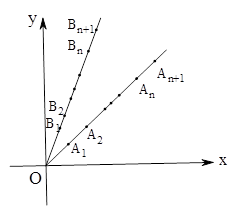
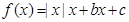 ,则下列命题中正确命题的序号有__________.
,则下列命题中正确命题的序号有__________.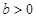 时,函数
时,函数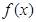 在R上是单调增函数;
在R上是单调增函数;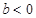 时,函数
时,函数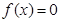 可能有三个实数根.
可能有三个实数根.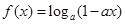 在区间
在区间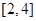 上是增函数,则实数
上是增函数,则实数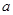 的取值范围是 。
的取值范围是 。 ;
;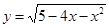 的递增区间是( )
的递增区间是( ) 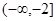
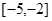
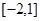
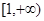
 ,则( )
,则( ) 上递增
上递增 上递增
上递增