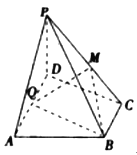
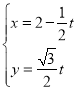题目内容
【题目】如图, ![]() 中,
中, ![]() 是
是![]() 的中点,
的中点, ![]() ,
, ![]() .将
.将![]() 沿
沿
![]() 折起,使
折起,使![]() 点与图中
点与图中![]() 点重合.
点重合.
(Ⅰ)求证:![]() ;
;
(Ⅱ)当三棱锥![]() 的体积取最大时,求二面角
的体积取最大时,求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在(Ⅱ)的条件下,试问在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?证明你的结论.
?证明你的结论.
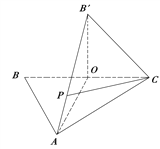
【答案】(Ⅰ)![]() 点,
点,
![]() 即
即![]() ,
,
又∵![]() ;
;
(Ⅱ)![]() ;(Ⅲ)存在,且为线段
;(Ⅲ)存在,且为线段![]() 的中点
的中点
证明如下:设![]() ,
,
![]()
又平面![]() 的法向量
的法向量![]() ,依题意得
,依题意得
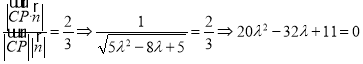
解得![]() 舍去).
舍去).
【解析】试题分析:(Ⅰ)欲证![]() ,需证明
,需证明![]() 垂直平面
垂直平面![]() 内两条直线,
内两条直线,
在三角形ABC中,因为![]() ,
, ![]() 是
是![]() 的中点,所以
的中点,所以![]() ;
;
又因为在折叠的过程中,![]() 保持不变,即
保持不变,即![]() ,
,![]() ,
,
所以结论成立;
(Ⅱ)在平面![]() 内,作
内,作![]() 于点
于点![]() ,则由(1)及已知可得当
,则由(1)及已知可得当![]() 与
与![]() 重合时,三棱锥
重合时,三棱锥![]() 的体积最大,并过
的体积最大,并过![]() 点作
点作![]() 于点
于点![]() ,连
,连![]() ,则
,则![]() 为
为![]()
在![]() 中,易得
中,易得![]() 的值,即为所求;
的值,即为所求;
(Ⅲ)根据图形及已知条件分析可得,存在线段![]() 上中点
上中点![]() ,使
,使![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,求出平面
,求出平面![]() 的法向量
的法向量![]() ,根据
,根据![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() 建立等式关系,即可求得结论.
建立等式关系,即可求得结论.

试题解析:(Ⅰ) ![]() 点,
点,
![]() 即
即![]() ,
,
又∵![]() ;
;
(Ⅱ)在平面![]() 内,作
内,作![]() 于点
于点![]() ,则由(Ⅰ)可知
,则由(Ⅰ)可知![]()
又![]() ,
, ![]() ,即
,即![]() 是三棱锥
是三棱锥![]() 的高,
的高,
又![]() ,所以当
,所以当![]() 与
与![]() 重合时,三棱锥
重合时,三棱锥![]() 的体积最大,
的体积最大,
过![]() 点作
点作![]() 于点
于点![]() ,连
,连![]() ,由(Ⅰ)知
,由(Ⅰ)知
![]() ,
, ![]()
![]()
![]() 为
为![]()
![]() ,
, ![]()
![]()
(Ⅲ)存在,且为线段![]() 的中点
的中点
证明如下:设![]() ,
,
![]()
又平面![]() 的法向量
的法向量![]() ,依题意得
,依题意得
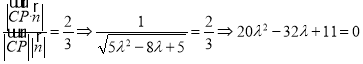
解得![]() 舍去).
舍去).

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目