题目内容
14.记直线x-3y-1=0的倾斜角为α,曲线y=lnx在(2,ln2)处切线的倾斜角为β.则α-β=-arctan$\frac{1}{7}$.分析 求出曲线y=1nx在(2,1n2)处切线斜率,从而可得tanα=$\frac{1}{3}$,tanβ=$\frac{1}{2}$,利用差角的正切公式,即可求出α-β.
解答 解:∵y=1nx,∴y′=$\frac{1}{x}$,
x=2时,y′=$\frac{1}{2}$,
∵直线x-3y-l=0的倾斜角为α,曲线y=1nx在(2,1n2)处切线的倾斜角为β,
∴tanα=$\frac{1}{3}$,tanβ=$\frac{1}{2}$,
∴tan(α-β)=$\frac{tanα-tanβ}{1+tanαtanβ}$=-$\frac{1}{7}$,
∵0<α<β<$\frac{π}{2}$,
∴α-β=-arctan$\frac{1}{7}$.
故答案为:-arctan$\frac{1}{7}$.
点评 本题考查导数的几何意义,考查斜率与倾斜角之间的关系,考查和角的正切公式,确定tanα=$\frac{1}{3}$,tanβ=$\frac{1}{2}$,是解题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
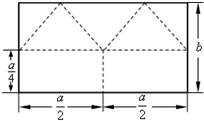 边长分别为a、b的矩形,按图中所示虚线剪裁后,可将两个小矩形拼接成一个正四棱锥的底面,其余恰好拼接成该正四棱锥的4个侧面,则$\frac{b}{a}$的取值范围是($\frac{1}{2}$,+∞).
边长分别为a、b的矩形,按图中所示虚线剪裁后,可将两个小矩形拼接成一个正四棱锥的底面,其余恰好拼接成该正四棱锥的4个侧面,则$\frac{b}{a}$的取值范围是($\frac{1}{2}$,+∞).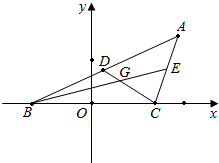 如图,在△ABC中,B(-1,0),C(1,0),CD、BE分别是△ABC的两条中线且相交于点G,且|CD|+|BE|=6.
如图,在△ABC中,B(-1,0),C(1,0),CD、BE分别是△ABC的两条中线且相交于点G,且|CD|+|BE|=6.